Funktionaler Zusammenhang
Das formale Strommodell setzt sich im Kern aus drei Gleichungen zusammen, welche alle die gleiche Struktur aufweisen. Einzige Ausnahme bildet der Wertebereich von Kt, welcher grösser ist als derjenige von "It-It-1" und "Ft-Ft-1" (vgl. dazu den vorhergehenden Abschnitt).
Im folgenden wird untersucht, welche Annahmen (oder Konsequenzen - je nach Sichtweise) mit den funktionalen Zusammenhängen, wie sie in [Kreutzberg, 1998] vorausgesetzt werden, verbunden sind. Dabei wird die Funktion zur Berechnung der Fachabteilungsquote betrachtet, wobei wegen der ähnlichen Struktur die Überlegungen analog für die Quote der Informatik-abteilung und des Erfahrungspools gelten.
Bei der Analyse des funktionalen Zusammenhangs kann sofort festgestellt werden, dass die Fachabteilungsquote von zwei endogenen Variablen abhängig ist: Zum einen wirkt sich die Gesamtkostenwachstumsrate Kt (ehemalige Umsatzwachstumsrate) auf die Quote der Fachabteilung aus, zum anderen beeinflusst der Wert aus der Vorperiode diese Quote.
Abbildung 13 zeigt anhand zweier Beispiele, welcher funktionale Zusammenhang zwischen den Variablen Kt und Ft besteht:
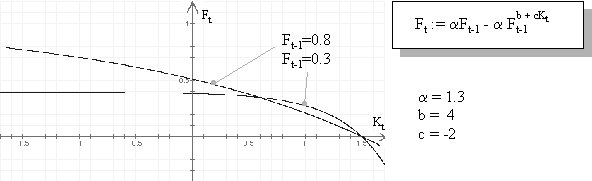
Abbildung 13: Einfluss der Kostenwachstumsrate auf die Fachabteilungsquote
Der Nichtlinearitätsfaktor muss grösser als eins sein, damit die Quote positive Werte annehmen. Im Beispiel ist das der Fall, wenn Kt kleiner als "1.5" ist. Der Nichtlinearitätsfaktor wird bei den obigen Funktionen immer grösser als eins sein, da Kt aufgrund der Definition nie Werte grösser als eins annehmen kann. Der Kurvenverlauf in Abbildung 13 ist somit für Werte grösser als eins uninteressant (sowohl Abszisse als auch Ordinate). Zur Berechnung der Informatik- und Erfahrungspoolquote sind Werte kleiner als "-1" auf der Abszisse ebenfalls unbedeutend (vgl. Abschnitt "Nichtlinearitätsfaktor"). Der funktionale Zusammenhang gilt also nur in einem eingeschränkten Bereich.
Das Beispiel deutet darauf hin, dass mit zunehmender Gesamtkostenwachstumsrate Kt die Quote der Fachabteilung sinkt. In [Kreutzberg, 1998; S. 29] wird dieser Zusammenhang mathematisch hergeleitet und durch verschiedene Argumente begründet.
Neben der Gesamtkostenwachstumsrate wird die Quote durch ihren Wert in der vorhergehenden Zeitperiode beeinflusst. Abbildung 14 zeigt Beispiele für den Zusammenhang zwischen "Ft" und "Ft-1":
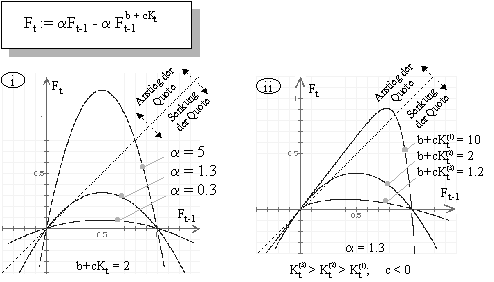
Abbildung 14: Einfluss der vorhergehenden Zeitperiode auf die Quote
Aus der Abbildung ist ersichtlich, dass zwischen den beiden Variablen "Ft" und "Ft-1" ein nichtlinearer Zusammenhang besteht. Die punktierten Geraden (Steigung gleich eins) bedeuten einen linearen Verlauf zwischen "Ft" und "Ft-1", wobei sich bei dieser linearen Funktion die Quoten im Laufe der Zeit weder erhöhen noch senken. Lineare Funktionen sind im Strommodell per Definition ausgeschlossen. Aufgrund der punktierten Geraden lässt sich sofort ablesen, ob die Quote gegenüber der Vorperiode steigt oder sinkt: Befindet sich der Kurvenverlauf bei der betreffenden Quote oberhalb der Geraden, so impliziert dies eine Steigerung gegenüber der Vorperiode. Verläufe unterhalb der punktierten Linie bewirken, dass der Wert der Quote tiefer liegt als in der Vorperiode.
Abbildung 14 (i) lässt vermuten, dass abhängig von der Wahl von a unter Umständen die Quote im Laufe der Zeit gar nie ansteigt. Um diesen Fall zu vermeiden, fordert [Kreutzberg, 1998] für den Parameter a , dass er grösser als eins ist. Diese Bedingung ist notwendig und hinreichend, damit die Quote zumindest bei kleinen Werten ansteigt (vgl. mathematische Begründung im Anhang). Der Kurvenverlauf aus Abbildung 14 (i) für "a = 0.3" wird somit ausgeschlossen.
Die Abbildung zeigt aber auch, dass der Kurvenverlauf für "a = 5" zu Widersprüchen führt: Obwohl a , Ft-1 und der Nichtlinearitätsfaktor gültige Werte annehmen, ergibt sich für gewisse Wertebereiche von Ft-1 eine Fachabteilungsquote Ft grösser als eins, was per Definition nicht sein darf. Es muss deshalb zusätzlich gefordert werden, dass "a Ft-1-a Ft-1^(b+cKt)" kleiner als eins ist.
Je nach Wahl des Parameters a und der Höhe des Nichtlinearitätseffekts stellt sich für die Quote eine obere Grenze tiefer als eins ein. Diese Annahme ist plausibel, denn es ist gut denkbar, dass eine Abteilung ceteris paribus nie eine Quote von beinahe 100% erreicht.
Aus der Abbildung 14 geht hervor, dass Quoten in der Nähe von eins sehr stark "gedämpft" werden: Der funktionale Zusammenhang bewirkt, dass eine hohe Quote innerhalb einer Periode immer auf einen Wert nahe bei null sinkt.
Die Vergangenheit bestimmt die Gegenwart. Insofern kann der Einbezug von Werten aus vorangegangenen Zeitabschnitten dazu dienen, Anhaltspunkte für die gegenwärtige und zukünftige Entwicklung zu geben. Dabei wird von einem kontinuierlichen Verlauf aufgrund der Vergangenheit ausgegangen, sofern keine tiefgreifenden Argumente dagegen sprechen. Für die Abbildung 14 würde dies bedeuten, dass sich die Werte der Funktion in der "Nähe" der gepunkteten Gerade befinden. Dies trifft im Strommodell insbesondere bei hohen Werten von "Ft-1" nicht zu.
Die Funktion zur Berechnung von "Ft" aufgrund von "Ft-1" hat folgende Eigenschaften (vgl. Anhang zur mathematischen Begründung):
Bei tiefen Quoten ergeben sich für die nächste Zeitperiode wiederum Quoten in der Nähe von null. Auf Abbildung 14 bezogen bedeutet dies bildlich gesprochen, dass bei tiefen Quoten der Kurvenverlauf der Funktion nahe der gepunkteten Geraden verläuft. Der Parameter a wird wegen den geforderten Bedingungen einen Wert grösser als eins aufweisen. Deshalb werden die tiefen Quoten im Laufe der Zeit ansteigen. Aufgrund des Dämpfungseffekts wird dieses Wachstum sich aber einstellen. Da in Abbildung 14 die gepunktete Gerade die "Gleichgewichtssituation" beschreibt, stellt auch der entsprechende Wert von "Ft-1" beim Schnittpunkt der Kurve mit der Geraden ein Gleichgewicht dar. Nimmt die Quote diesen Wert an, so wird er sich ceteris paribus nicht mehr ändern.
Nimmt die Quote (Ft-1) Werte höher als im Gleichgewichtspunkt an, so wird der Wert in der nächsten Periode (Ft) kleiner sein. Hohe Quoten werden in der nächsten Periode wieder nahe bei null liegen, und somit wird insbesondere ausgeschlossen, dass die Quoten ceteris paribus in zwei aufeinanderfolgenden Perioden hohe Werte annehmen.
Es gilt zu beachten, dass sich dieser Verlauf sowohl bei einem konstanten Gesamtkosten-Wachstum wie bei einer konstanten Gesamtkosten-Senkung als auch bei stagnierenden Gesamtkosten ergibt (vgl. Abbildung 14 - ii). Der beschriebene Verlauf resultiert, wenn Kt konstant ist, egal welchen Wert dabei Kt besitzt:
Dieser Sachverhalt ist darauf zurückzuführen, dass die Parameter des Nichtlinearitätsfaktors ohne grosse Einschränkung gewählt werden dürfen. So resultiert beispielsweise bei einem 10-prozentigen Anstieg der Kosten (Kt=0.1) und mit "b=3, c= -10" ein Nichtlinearitätsfaktor von zwei. Dasselbe Ergebnis wird erhalten, wenn sich die Kosten um 10 Prozent senken (Kt= - 0.1) und b gleich eins sowie c gleich "-10" gesetzt werden. Es besteht in beiden Fällen der gleiche Zusammenhang zwischen "Ft-1" und "Ft".
Wie die obigen Überlegungen zeigen, ist der funktionale Zusammenhang zwischen "Ft-1" und "Ft" insbesondere bei hohen Quoten schwierig zu begründen und mit Problemen behaftet: So wird unabhängig von der Kostenentwicklung eine Quote mit hohem Wert in der nächsten Periode immer einen Wert nahe bei null aufweisen, wobei sich dieser Wert in der darauffolgenden Periode in jedem Fall erhöhen wird, aber nur ein wenig.
Es ist jedoch gerade der nichtlineare Zusammenhang zwischen den Quoten, welcher für Änderungen der Quoten verantwortlich ist. Starke Schwankungen resultieren vor allem, wenn die Quoten hohe Werte erreichen und dadurch in der nächsten Periode wieder tief ausfallen. Je nach Wahl der Parameter und der exogenen Variablen wird im Strommodell eine Annäherung an den Extremwert von eins erreicht, wodurch der Wert der Quote stark gesenkt wird und diese Schwankung zudem in die nächste Gleichung einfliesst (vgl. [Kreutzberg, 1998; S. 41f., S. 45 f.]).
Entwicklung der Quoten im Laufe der Zeit und Gleichgewicht
[Kreutzberg, 1998] stellt bei der logischen Analyse des Strommodells fest, dass die Entwicklung der Quoten je nach Wahl der Parameter "gleichgewichtig und stabil" verläuft oder "ein deterministisches Chaos" resultiert. Die gefundenen Ergebnisse basieren auf Computersimulationen.
Im folgenden wird die Entwicklung der Quoten im Laufe der Zeit zuerst mit einem anderen Ansatz analysiert: Es wird der funktionale Zusammenhang zwischen Ft und Ft-1 in Anlehnung an das vorhergehende Unterkapitel und im Hinblick auf ein Gleichgewicht untersucht. Dabei wird zunächst von einem konstanten Nichtlinearitätsfaktor ausgegangen.
Im weiteren Verlauf der Arbeit wird als Gleichgewichtspunkt F* einer Quote derjenige Wert verstanden, bei welchem sich die Quote gegenüber allen künftigen Zeitperioden nicht verändert. Die Fachabteilungsquote befindet sich im Gleichgewicht, wenn in jedem künftigen Zeitpunkt die Bedingung "Ft = Ft-1 (=F*)" gilt. Analog wird der Gleichgewichtspunkt für die Quote der Informatikabteilung und des Erfahrungspools definiert. Bei den nachfolgenden Betrachtungen wird primär die Fachabteilungsquote betrachtet, doch die Erkenntnisse lassen sich ebenso auf die anderen Quoten übertragen.
Bei gegebenem Parameter a und konstantem Nichtlinearitätsfaktor lässt sich der Gleichgewichtspunkt berechnen durch (math. Begründung im Anhang):
![]()
Der Gleichgewichtspunkt ist unter den Voraussetzungen des nichtlinearen Modells von [Kreutzberg, 1998] eindeutig. Nimmt der Startwert " F0" diesen Wert an, so wird sich die Quote im Laufe der Zeit ceteris paribus nie ändern. Es stellt sich natürlich sofort die Frage, was geschieht, wenn der Initialwert der Quote nicht im Gleichgewicht liegt.
Das formale Strommodell berücksichtigt den Zeitaspekt, und bei gegebenen exogenen Variablen kann die Entwicklung der Fachabteilungsquote über die Zeit abgeleitet werden. Grundsätzlich sind drei Möglichkeiten bezüglich der Entwicklung einer Quote denkbar:
Der erste Fall tritt ein, wenn die Quote in der Vergangenheit exakt die benötigten Werte aufweist, um durch die Transformationen ("Ft = a Ft-1 -a (Ft-1^NLF)") schliesslich den Gleichgewichtspunkt zu erreichen. Der umgekehrte Weg kann eingeschlagen werden, wenn ausgehend vom Gleichgewichtspunkt F* berechnet wird, bei welchen Werten von Ft-1 gilt, dass Ft gleich F* ist. Dann wird analog berechnet, wie die Werte gewählt werden müssen, um Ft-1 zu erhalten und so weiter. Das Problem besteht bei diesem Lösungsansatz darin, dass sich der Berechnungsvorgang unter Umständen unendlich oft wiederholt und nicht alle Werte ermittelt werden können, welche schliesslich im Gleichgewicht enden.
Im zweiten Fall konvergiert die Quote im Laufe der Zeit an den Gleichgewichtspunkt. In folgenden Abschnitten wird eine hinreichende Bedingung für diesen Fall genannt.
Konvergiert die Quote nicht ins Gleichgewicht und nimmt sie den entsprechenden Wert nicht an, so stellt sich die Frage, ob trotzdem eine gewisse Regelmässigkeit in der Entwicklung der Quote auftritt. Die Quote könnte einen bestimmten Zyklus aufweisen oder sich einem solchen annähern.
Abbildung 15 illustriert anhand eines Beispiels, wie sich die Quote bei gegebenem Parameter a und Nichtlinearitätsfaktor entwickelt:
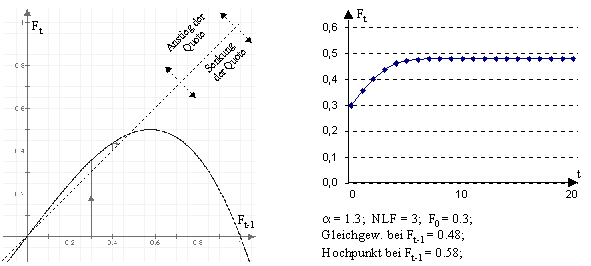
Abbildung 15: Gleichgewichtspunkt - Beispiel 1
Sämtliche Punkte auf der "45° -Geraden" in der Grafik auf der linken Seite der Abbildung 15 stellen Gleichgewichtspunkte dar. Der Schnittpunkt des Kurvenverlaufs mit dieser Geraden bildet den Gleichgewichtspunkt für die entsprechende Funktion, was im obigen Beispiel bei " F* = 0.4804" der Fall ist. Einzig die (gerundeten) Startwerte "F0 = 0.4804" und "F0 = 0.6692" werden im Beispiel den Gleichgewichtswert annehmen.
Wie aus der Abbildung hervorgeht, konvergiert die Fachabteilungsquote gegen den Gleichgewichtspunkt, wenn die Quote mit dem Wert "0.3" initialisiert wird. Die Grafik in Abbildung 15 deutet zudem darauf hin, dass sämtliche Startwerte konvergieren (mit Ausnahme der zuvor genannten Startwerte, welche exakt im Gleichgewichtswert F* verharren). Dieses Ergebnis kann abgeleitet werden, wenn der zeitliche Verlauf der Quote in der (linken) Grafik betrachtet wird:
Auf der Abszisse wird vom Startwert F0 ausgegangen. Der Wert der nächsten Zeitperiode kann aufgrund des Verlaufs der Funktion abgelesen werden. Der neu erhaltene Wert wird in der nachfolgenden Periode wieder als Ausgangswert (Ft-1) verwendet, um die Quote für die darauffolgende Zeitperiode (Ft) zu ermitteln. Dieser Wechsel von Ft zu Ft-1 wird in der Grafik dargestellt, durch die horizontalen Linien, welche mit der "45° -Geraden" geschnitten werden. Wird diese Vorgehensweise graphisch abgebildet, so resultiert schliesslich der "Zickzack-Verlauf" wie in der (linken) Grafik aus Abbildung 15. Im Beispiel wurde als Startwert eine Quote kleiner als der Gleichgewichtspunkt gewählt. Auch bei grösseren Werten wird sich die Quote an den Gleichgewichtspunkt annähern. Liegt der Startwert zwischen Gleichgewichtspunkt und Hochpunkt (Maximum), so wird sich die Quote "von oben" dem Gleichgewichtspunkt nähern; ansonsten werden die Werte schliesslich kleiner als F* sein und gegen den Gleichgewichtspunkt konvergieren.
Aufgrund des funktionalen Zusammenhangs zwischen Ft und Ft-1 verläuft die entsprechende Kurve bei tiefen Werten von Ft-1 immer über der gepunkteten Geraden, sie weist einen Hochpunkt auf, schneidet die gepunktete Gerade und verläuft bei hohen Werten von Ft-1 unterhalb der gepunkteten Geraden. Entscheidend ist für den allgemeinen Fall, ob sich der Hochpunkt vor oder nach dem Gleichgewichtspunkt befindet: Liegt der Hochpunkt wie im obigen Beispiel rechts vom Gleichgewichtspunkt, so wird die Quote sich dem Gleichgewichtszustand annähern. Eine hinreichende Bedingung, damit die Quote konvergiert, ist somit:
a + NLF - a (NLF) > 0
(mathematische Begründung bezüglich der Lage von Hochpunkt und Gleichgewichtspunkt im Anhang)
Falls der Gleichgewichtspunkt mit dem Hochpunkt zusammenfällt, wird die Quote ebenfalls in Richtung Gleichgewicht konvergieren; bei Startwerten grösser als F* wird die Quote im Zeitpunkt "t=1" und allen darauffolgenden Perioden kleiner als der Gleichgewichtspunkt sein.
Wesentlich schwieriger ist es, Aussagen über die Entwicklung der Quote zu machen, wenn sich der Hochpunkt (Maximum) der Funktion bei tieferen Werten als der Gleichgewichtspunkt befindet. Dies ist der Fall, wenn die folgende Bedingung erfüllt ist:
a + NLF - a (NLF) < 0
Abbildung 16 zeigt ein Beispiel, bei welchem die Quote nicht gegen den Gleichgewichtspunkt konvergiert:
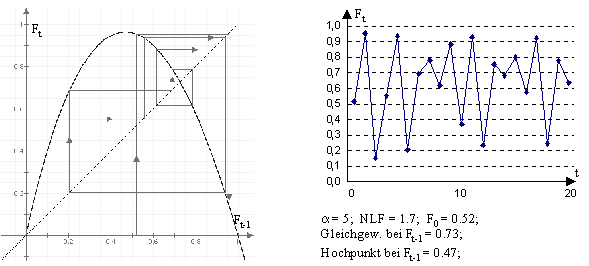
Abbildung 16: Gleichgewichtspunkt - Beispiel 2
Es ist nicht sofort ersichtlich, ob die Quote bei ihrer Entwicklung gewisse Regelmässigkeiten aufweist. Weiter gilt zu beachten, dass sich die Quote dem Gleichgewichtspunkt annähert und sich anschliessend wieder entfernt.
Für das obige Beispiel scheint sich die Quotenentwicklung ab dem Zeitpunkt "t=70" einem Zyklus anzunähern, welcher sich jeweils nach drei Perioden wiederholt und nicht gegen das Gleichgewicht konvergiert. Zudem lässt die Computersimulation vermuten, dass sämtliche Quoten mit beliebigen Startwerten im selben Zyklus münden (mit Ausnahme derjenigen Werte, welche exakt ins Gleichgewicht abgebildet werden).
Als Beispiele für (gerundete) Startwerte, welche die Quote ins Gleichgewicht überführen, können aufgelistet werden: F0 = 0.72703 / 0.22402 / 0.05120 / 0.93204 / 0.01068.
Von zentraler Bedeutung für die Entwicklung der Quote ist, welchen Wert die Ableitung erster Ordnung der Funktion (Steigung) im Gleichgewichtspunkt besitzt. Wie bereits beschrieben, wird die Quote bei Werten grösser oder gleich null konvergieren. Liegt die Steigung im Intervall "-1 bis 0", so wird die Quote ab einem gewissen "Einzugsgebiet" des Gleichgewichts (Werte nahe bei F*) ebenfalls konvergieren. Dies lässt sich aufgrund analoger Überlegungen begründen, wie zuvor bei der Herleitung für die hinreichende Bedingung zum Konvergieren. Zahlreiche Computersimulationen deuten zudem darauf hin, dass das "Einzugsgebiet" bei allen Startwerten erreicht wird und dass somit eine kontinuierliche Annäherung an den Gleichgewichtspunkt stattfindet, wenn gilt:
-1 < a + NLF - a (NLF) < 0
Weiter lassen Computersimulationen vermuten, dass bei einer Steigung von "-1" ebenfalls eine kontinuierliche Annäherung resultiert.
Es kann festgehalten werden, dass sich die Quote in der Nähe von F* wieder vom Gleichgewicht entfernen wird, wenn die Steigung der Funktion kleiner als "-1" ist. Abbildung 17 zeigt anhand eines Beispiels den typischen Verlauf der Quote, wie er nahe bei F* immer resultieren wird, wenn die Steigung kleiner als "-1" ist:

Abbildung 17: Entfernung der Quote vom Gleichgewicht
Es stellt sich natürlich sofort die Frage, wie sich die Quote entwickelt, wenn sie nicht ins Gleichgewicht konvergiert. Zahlreiche Computersimulationen deuten darauf hin, dass sich vor allem bei stark negativen Werten des Ausdrucks "a + NLF - a (NLF)" unregelmässige Entwicklungen für die Quoten ergeben. Weiter wird vermutet, dass bei einer Steigung der Funktion (im Gleichgewicht) nahe bei "-1" (und kleiner als "-1") die Quote sich einem eindeutigen Zyklus annähert oder diesen annimmt.
Im Anhang sind einige ausgewählte Beispiele zur Entwicklung der Quote aufgelistet. Die Ergebnisse basieren teilweise auf Computersimulationen, teilweise werden sie in dieser Arbeit mathematisch/logisch begründet. Mit der Methode "Simulation" sind einige Probleme verbunden (vgl. dazu ebenfalls Anhang), weil immer "nur" Beispiele getestet werden und somit der Schluss auf die Allgemeinheit nicht zulässig ist. In diesem Sinne dürfen die Ergebnisse der Computersimulation lediglich als ein erster Eindruck verstanden werden.
Die bisherigen Untersuchungen in diesem Kapitel gehen davon aus, dass der Nichtlinearitätsfaktor sich im Laufe der Zeit nicht ändert. Bei der Berechnung der Fachabteilungsquote beeinflussen die Unternehmensgesamtkosten den Nichtlinearitätsfaktor. In ähnlicher Weise ist der Nichtlinearitätsfaktor der Quote der Informatikabteilung und des Erfahrungspools von der Veränderung anderer Quoten abhängig. Daraus lässt sich ableiten, dass der Nichtlinearitätsfaktor im allgemeinen nicht konstant ist und typischerweise sogar in jeder Periode einen anderen Wert annehmen wird. Eine Veränderung des Werts des Nichtlinearitätsfaktors bedeutet jedoch, dass sich der Gleichgewichtspunkt verschieben wird.
In Abbildung 18 wird ein Beispiel vorgestellt, bei welchem der Nichtlinearitätsfaktor im Zeitpunkt "t=5" seinen Wert ändert:
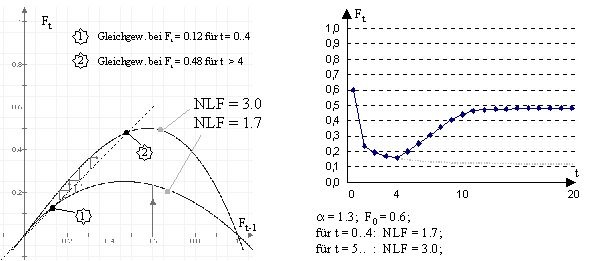
Abbildung 18: Gleichgewichtspunkt - Beispiel 3
Initiiert wird die Quote mit dem Wert "0.6", und der Nichtlinearitätsfaktor weist zu Beginn einen Wert von "1.7" auf. Bei dieser Ausgangslage konvergiert die Fachabteilungsquote gegen den Wert "F* = 0.12". Im Beispiel wird angenommen, dass zum Zeitpunkt "t=5" die Unternehmens-Gesamtkostenwachstumsrate sinkt, wodurch sich der Nichtlinearitätsfaktor erhöht. Dadurch wird eine Verschiebung des Gleichgewichts hervorgerufen. Die Quote konvergiert nun neu ab dem betreffenden Zeitpunkt gegen den Wert "F* = 0.48". Es wird jedoch nicht immer so sein, dass sich nach der Änderung des Nichtlinearitätsfaktors wieder eine Annäherung an ein Gleichgewicht einstellt. Steigt im obigen Beispiel der Nichtlinearitätsfaktor auf einen Wert von "10" an, so ist keine kontinuierliche Annäherung an ein Gleichgewicht erkennbar.
Wenn sich der Nichtlinearitätsfaktor ständig ändert, wird der Gleichgewichtspunkt ebenfalls wechseln, so dass eine sukzessive Annäherung der Quote an einen Gleichgewichtspunkt im allgemeinen verunmöglicht wird.
Ein interessanter Spezialfall ergibt sich, wenn die Kostenwachstumsrate Kt (exogene Variable) als konstant betrachtet wird. Bei geeigneter Wahl des Parameters a und Kt wird die Fachabteilungsquote gegen ein Gleichgewicht konvergieren (vgl. Bedingung für Gleichgewicht). Die Differenz der Fachabteilungsquote aus zwei Zeitperioden (Ft-Ft-1) wird sich somit dem Wert null annähern. Dies bedeutet aber wiederum, dass der Nichtlinearitätsfaktor der Informatikabteilung gegen einen konstanten Wert konvergiert. Abhängig von diesem Wert und vom Parameter b kann sich auch die Informatikabteilung - zeitverzögert - in ein Gleichgewicht "einpendeln". In diesem Sinne kann die Differenz "Ft-Ft-1" als Beitrag der Fachabteilung zur Stabilität der Informatikabteilung interpretiert werden, während durch den Parameter b der Beitrag der Informatikabteilung zu einem Gleichgewicht ausgedrückt wird. (Stabilität wird hier verstanden als kontinuierliche Annäherung an ein Gleichgewicht, wobei die Änderungen der Quoten sehr klein sind.)
Analoge Ergebnisse gelten für den Erfahrungspool: Nähert sich die Informatikabteilungsquote an ein Gleichgewicht, so wird sich bei geschickter Wahl des Parameters c die Erfahrungspoolquote ebenfalls kontinuierlich und wiederum zeitverzögert in ein Gleichgewicht einpendeln.
Somit kann festgehalten werden, dass die Kostenwachstumsrate Kt des Unternehmens sowie deren Veränderung (neben a , b , c ) einen entscheidenden Einfluss auf die Stabilität sowohl der Fachabteilung als auch der Informatikabteilung wie des Erfahrungspools hat. Eine Änderung der Kostenwachstumsrate Kt wird sich zunächst am Stärksten auf die Fachabteilungsquote auswirken, während die Quote der Informatikabteilung beziehungsweise des Erfahrungspools indirekt und in abgeschwächter Form betroffen ist.
Weiter geht aus der Analyse des Strommodells hervor, dass die Informatikabteilungsquote sich nur dann stabil entwickeln kann, wenn die Quote der Fachabteilung dies ebenfalls macht. Notwendige Bedingung für einen stabilen Verlauf der Erfahrungspoolquote ist, dass sich die Quoten der Informatik- und Fachabteilung zuerst in ein Gleichgewicht "einpendeln".
Bei der Analyse über die Entwicklung der Quoten stellt sich die Frage, was für Konsequenzen unterschiedliche Startwerte haben. Insbesondere interessiert, ob kleine Änderungen in den Anfangswerten grosse Änderungen in den Ergebnissen bewirken.
Wie bereits vorher abgeleitet, wird die Quote unabhängig vom Initialwert konvergieren, falls folgende Bedingung erfüllt ist:
a + NLF - a (NLF) ³ 0
Bei denjenigen Werten der Quote, bei welchen die erste Ableitung der entsprechenden Funktion einen absoluten Wert grösser als eins aufweist, werden unterschiedliche Eingabewerte stärkere Abweichungen zur Folge haben. Bei tiefen Quoten ist dies bei hohem Wert des Parameters a der Fall. Zudem bewirkt ein hoher Wert des Nichtlinearitätsfaktors und des Parameters a , dass die erste Ableitung der Funktion bei hohen Quoten stark negativ ist, wodurch geringfügige Änderungen der Quote eine hohe Differenz in der nächsten Zeitperiode bewirken.
Es ist nicht bekannt, ob sich die Quote unter der Bedingung "a + NLF - a (NLF) < -1" einem eindeutigen Zyklus annähert. Die zahlreichen Computersimulationen lassen vermuten, dass beide Fälle eintreten können. Für den Fall, dass sich die Quote bei gegebenem a und NLF keinem eindeutigen Zyklus annähert oder diesen annimmt, werden kleine Änderungen in den Anfangsbedingungen zu sehr unterschiedlichen Entwicklungen der Quote führen - dies vor allem bei hohen Quoten und stark negativen Werten des Ausdrucks "a + NLF - a (NLF)".
Logische Analyse der Gleichungen (durch [Kreutzberg, 1998])
Die drei Gleichungen zur Herleitung der Quoten werden in [Kreutzberg, 1998] analysiert und die gefundenen Ergebnisse interpretiert. Funktionen werden dazu nach verschiedenen Variablen abgeleitet (math. Ableitungen erster Ordnung). Unter den Bedingungen, wie sie im formalen Strommodell gefordert werden, sind sämtliche mathematischen Schlussfolgerungen von [Kreutzberg, 1998] korrekt. Im Anhang sind die betreffenden mathematischen Umformungen aufgeführt und ergänzt.
Tabelle 9 fasst die wichtigen Ergebnisse verbal nochmals zusammen und nennt Argumente für und gegen diese Resultate:
|
Ergebnis der logischen Analyse der Gleichungen |
Bemerkungen |
|
"¶ Quotet / ¶ NLF>0": Eine Erhöhung des Nichtlinearitätsfaktors (NLFt) bewirkt eine Erhöhung der entsprechenden Quote (Ft / It / Et) |
Der Dämpfungseffekt, der den Anstieg der Quote bremst, sinkt mit steigendem Nichtlinearitätsfaktor. (vgl. [Kreutzberg, 1998; S. 29]) |
|
"¶ Ft / ¶ Kt <0": Eine Erhöhung der Kostenwachstumsrate (ehemals Umsatzwachstumsrate) bewirkt, dass die Fachabteilungsquote sinkt. |
Bei dieser Argumentation wird vorausgesetzt, dass der Umsatz und die Kosten ungefähr "parallel" verlaufen, und die Ausweitung des Geschäfts in der aktuellen Zeitperiode vollzogen wird (ansonsten bewirkt eine Erhöhung der Wachstumsrate, dass die Fachabteilungsquote erst in einer späteren Phase sinkt).
|
|
"¶ Ft / ¶ b >0": Eine Erhöhung des Parameters b bewirkt, dass die Quote der Fachabteilung ansteigt. |
|
|
"¶ WEFt / ¶ Ft-1 = a >0": Höhere Werte von Ft-1 bewirken einen grösseren Wachstumseffekt WEFt. |
|
|
"¶ It / ¶ Ft <0": Ein Anstieg der Fachabteilungsquote bewirkt, dass die Informatikabteilungsquote sinkt. |
|
|
"¶ Et / ¶ It <0": Eine Erhöhung der Informatikabteilungsquote bewirkt eine Senkung der Erfahrungspoolquote. |
|
|
"¶ Et / ¶ (It - It-1) <0": Bei einem Anstieg des Wachstums der Informatikabteilungsquote sinkt die Erfahrungspoolquote.
|
|
Tabelle 9: Bemerkungen zur logischen Analyse der Gleichungen
(Ergebnisse in Anlehnung an [Kreutzberg, 1998])
Grenzen des Modells
Aus dem grundlegenden Strommodell werden die Pole Fach- und Informatikabteilung sowie der Erfahrungspool ins formale Strommodell übernommen. Insbesondere wird die Einheit "Unternehmensleitung" im formalen Strommodell nicht berücksichtigt, was bedeutet, dass Führungskräfte (und deren Aufgaben) ab einer gewissen Hierarchiestufe aus dem formalen Strommodell ausgeschlossen sind. Leitende Instanzen der unteren Hierarchiestufen aus dem Fach- und Informatik-Bereich werden im Modell aber trotzdem den entsprechenden Abteilungen zugeordnet. Aufgrund der Notwendigkeit zur Abstraktion innerhalb eines jeden Modells kann es gerechtfertigt werden, dass das Modell die Frage offen lässt, bei welcher Hierarchiestufe die Grenze exakt gezogen wird. Es bleibt aber festzuhalten, dass das Top-Management, wie bereits erwähnt, aus dem formalen Strommodell ausgeschlossen ist.
Das formale Strommodell von [Kreutzberg, 1998] stellt den Umweltausschnitt mathematisch dar. Die drei Kern-Gleichungen zeigen den Zusammenhang zwischen den verschiedenen Abteilungen. Dabei wird jedem Pol in einem Zeitpunkt "t" ein entsprechender Wert zugeordnet, welcher die Ausprägung der betreffenden Einheit wiedergibt. Im Strommodell werden dazu die Quoten verwendet; sie informieren als einzige Grössen über den Zustand einer Abteilung in einem gegebenen Zeitpunkt.
Im grundlegenden Strommodell werden zahlreiche Verbindungen zwischen den verschiedenen Unternehmenseinheiten aufgezeigt. Diese Beziehungen werden zwecks Reduktion der Komplexität nicht allesamt übernommen. Das formale Strommodell beachtet den Einfluss der Unternehmens-Gesamtkosten auf die Fachabteilung, die Wirkung der Fachabteilung auf die Informatikabteilung sowie den Einfluss der Informatikabteilung auf den Erfahrungspool. Insbesondere wird die gegenseitige Beeinflussung der Pole nicht modelliert; der Erfahrungspool hat im formalen Strommodell keine Auswirkungen auf die Entwicklung der anderen Abteilungen, und die Informatikabteilung beeinflusst die Entwicklung der Fachabteilung nicht.
Die oben aufgeführten Bemerkungen sind zu berücksichtigen, wenn es darum geht, aufgrund von simulierten/prognostizierten Verläufen der Quoten auf die Entwicklung des Unternehmens oder des Informationsmanagements zu schliessen. Schwierigkeiten treten dabei insbesondere mangels eindeutiger Indikatoren auf:
Aufgrund der Definition der Quote und der Zusammensetzung der drei Pole stehen die Quoten indirekt in Zusammenhang mit dem Informationsmanagement (vgl. Abschnitt "Quoten"). Zwar kann angenommen werden, dass Quoten durch das Informationsmanagement in der einen oder anderen Form beeinflusst werden, doch sind Rückschlüsse aufgrund der Simulationswerte auf die Entwicklung des Informationsmanagements problematisch und nicht präziser als Erkenntnisse bezüglich der allgemeinen Unternehmensentwicklung.
Als Grundlage für Aussagen über die langfristige Entwicklung des Unternehmens dient im formalen Strommodell die Höhe der einzelnen Quoten und deren Veränderung im Laufe der Zeit.
Der ideale Wert für die Quoten kann jedoch theoretisch nicht abgeleitet werden und ist insbesondere nicht eins: So bedeutet eine Informatikabteilungsquote von "It =0.99", dass 99 Prozent der Kosten der Fachabteilung dem Bezug von Informatik-Leistungen zuzurechnen sind. Hohe Quoten sind somit normalerweise nicht anzustreben. Andererseits besagt eine Informatikabteilungsquote von "It =0.01", dass nur ein Prozent der Fachabteilungskosten dem Bezug von Informatik-Produkten zuzuschreiben ist. Es kann somit festgehalten werden, dass Quoten normalerweise keine Extremwerte annehmen sollten, dass aber im allgemeinen auch kein "geeigneter/anzustrebender" Wert existiert. Verschiedene Konstellationen der Quoten können sich günstig (oder ungünstig) auf das Unternehmen auswirken, wobei dies anhand des 3-Tupels nicht ohne weitere Kenntnisse entschieden werden kann. Sind beispielsweise im Zeitpunkt "t" alle drei Quoten gleich "0.5", so könnte dies für ein konkretes Unternehmen sowohl positiv als auch negativ sein. Anhaltspunkte könnten hier unter Umständen empirisch ermittelte Branchenwerte liefern.
Als Beurteilungskriterium zur positiven Entwicklung der Unternehmung aufgrund von Simulationswerten (Prognosewerten) verbleibt somit die Veränderung der Quoten im Laufe der Zeit. Dabei gilt es die folgenden Aspekte zu berücksichtigen:
Variieren die Werte der Quoten innerhalb eines kurzen Zeitraums sehr stark, so wird dies für die Unternehmung normalerweise nachteilig sein: Die Einheiten des Unternehmens ändern ihre Kostenanteile massiv, wodurch bei unregelmässigen Verläufen die Planung erschwert wird. Zudem ist bei derartigen Veränderungen der Kostenstruktur davon auszugehen, dass das Arbeitsvolumen der einzelnen Abteilungen im Laufe der Zeit sehr unterschiedlich anfällt, wodurch die optimale Auslastung der Ressourcen erschwert oder sogar verunmöglicht wird.
Wenn eine Quote innerhalb eines Zeitraums "gemässigt" ansteigt (oder sinkt), so kann ohne zusätzliche Kenntnisse nicht beurteilt werden, ob dieser Verlauf sich positiv oder negativ auf die Unternehmung auswirkt (weil der optimale Wert einer Quote theoretisch nicht zu ermitteln ist). Nähert sich der Verlauf einer Quote einem Zyklus an oder entwickelt sie sich unregelmässig, so ist "lediglich" bei starken Schwankungen von einer negativen Entwicklung auszugehen. Allerdings gilt es dabei zu beachten, dass insbesondere unregelmässige Verläufe der Quoten mit starken Schwankungen verbunden sind.
Bei ständig ändernden Gesamtkostenwachstumsraten Kt wird keine Quote gegen ein Gleichgewicht konvergieren (vgl. Kapitel "Entwicklung der Quoten im Laufe der Zeit und Gleichgewicht"). Sämtliche Quoten werden ihre Werte fortlaufend wechseln. Dabei ist die Veränderung der Nichtlinearitätsfaktoren (speziell der Fachabteilung) für die Höhe der Schwankungen der Quoten ausschlaggebend (insbesondere der Parameter c).
Folgende Hypothesen ergeben sich zur Beurteilung der langfristigen Entwicklung des Unternehmens, wenn die Simulationswerte der Quoten ermittelt sind:
|
Unternehmen überlebt langfristig (+)
|
Unternehmen wird langfristig nicht überleben (-) |
|
|
Notwendige Bedingungen: |
|
|
|
Hinreichende Bedingungen: |
|
Tabelle 10: Langfristige Entwicklung der Unternehmung
Weitreichende Konsequenzen ergeben sich aus der Tatsache, dass der Erfahrungspool im formalen Strommodell keine Begründung zur Entwicklung der anderen Unternehmensteile liefert (vgl. Kapitel "Kausalitätsstruktur"):
Wie im Kapitel "Grundlegendes Strommodell" aufgezeigt wird, setzt sich der Erfahrungspool unter anderem aus "Wissen und Fertigkeiten der Informatikmitarbeiter für künftige Arbeiten", "Erfahrungsdatenbank" und "Projektcontrolling" zusammen. Der Erfahrungspool wird aufgrund des gewählten Abstraktionsniveaus im nichtlinearen Modell von [Kreutzberg, 1998] nicht weiter unterteilt. Die betreffende Quote Et bezieht sich somit nicht auf einzelne Elemente sondern den Pool als Ganzes. Eine Erfahrungspoolquote von beispielsweise "Et=0.5" bedeutet, dass 50 % der Informatikkosten in den Pool investiert werden. Allerdings kann aus diesem Wert nicht abgelesen werden, welche Anteile dabei auf das Projektcontrolling, die Erfahrungsdatenbank und das Wissen der Mitarbeiter entfallen. Um zu gesonderten Aussagen bezüglich der jeweiligen Elemente des Erfahrungspools zu gelangen, muss der Erfahrungspool unterteilt werden, wie dies beispielsweise im Kapitel "Grundlegendes Strommodell / Erfahrungspool" vorgeschlagen wird (vgl. Abbildung 8; Elemente des Erfahrungspools).
Die Projektmitglieder informieren über ihre Tätigkeiten sowie den Verlauf des Projekts und liefern Daten für die Erfahrungsdatenbank. Die Kosten zur Bereitstellung dieser Daten sind in der Erfahrungspoolquote enthalten. Oft werden die betreffenden Daten durch den Projektcontroller verdichtet und aufbereitet. Die dabei anfallenden Kosten, das heisst die Investitionskosten des Projektcontrollings in den Erfahrungspool, sind jedoch in der Quote nicht enthalten, weil es sich um Leistungsströme innerhalb des Pools handelt.
In den obigen Abschnitten wird argumentiert, dass die Aussagekraft der Entwicklung der Quoten mit Problemen behaftet und eingeschränkt ist. Hier gilt es zu beachten, dass die Untersuchungen in dieser Arbeit ausschliesslich auf theoretischen Überlegungen beruhen und keine empirischen Daten hinzugezogen werden. Zusätzliche Anhaltspunkte zur Beurteilung der Entwicklung der Quoten und Bewährung des Modells können empirische Erhebungen liefern.
Jedes Modell reduziert die Komplexität des darzustellenden Umweltausschnitts und stellt somit eine eingeschränkte Sichtweise dar. Je nach Problemstellung können Grenzen aufgelöst und andere neu gebildet werden. Das Strommodell von [Kreutzberg, 1998] ist ein offenes und flexibles Modell, weshalb im nächsten Kapitel basierend auf dem grundlegenden Strommodell unter anderem der Einfluss des Erfahrungspool auf die Informatikabteilung konkret (formal) untersucht wird. Nutzen und Kosten des Auftraggebers sowie die Arbeitsleistungen der Auftragempfänger werden mittels Prinzipal-Agent-Modellen untersucht.