3.2.2 Formales Strommodell
Die grossen Nachteile von verbalen Modellen sind "ihre Schwerfälligkeit, die Unmöglichkeit, viele logische und mathematische Analyseverfahren zu benutzen, und - daraus folgend - die mangelnde Präzision ihrer Schlussfolgerungen bzw. die Unmöglichkeit, überhaupt zu gewissen Schlussfolgerungen zu gelangen" ([Kleinewefers, 1983; S. 13]). Zu einer ähnlichen Erkenntnis kommt [Kreutzberg, 1998; S. 5]: "Die resultierenden Ansätze (aus der Literatur) für das Informationsmanagement lassen ... nur schwer eine Überprüfung auf Vollständigkeit und Korrektheit des Informationsmanagements zu." Das formale Strommodell soll diesem Manko entgegenwirken. Das Schwergewicht der Untersuchungen liegt deshalb auf dem formalen Modell. Das grundlegende, verbale Modell weist in dem Sinne ja ebenfalls die eingangs beschriebenen Nachteile auf und dient deshalb vor allem als Einstieg ins formale Strommodell.
Die Chaostheorie bildet die Grundlage für das nichtlineare Modell von [Kreutzberg, 1998]. Das Modell basiert also auf einer "mathematischen Theorie dynamischer Systeme, die diese Systeme durch deterministische, nichtlineare Differenzen- oder Differenzialgleichungen beschreibt. Wesentliches Charakteristikum chaotischer Systeme ist, dass die Zeitpfade der Variablen äusserst sensitiv auf Veränderungen der Anfangsbedingungen reagieren" ([Gabler, 1997]).
Das formale Strommodell berücksichtigt - wie weiter vorne bereits beschrieben - die Aspekte "Zeit", "Nichtlinearität" und "Determiniertheit". Der Bezug zur Chaostheorie ist gerechtfertigt.
Das nichtlineare Modell von [Kreutzberg, 1998] ist lediglich eine mögliche Ausprägung der Chaostheorie; es kann davon ausgegangen werden, dass andere Modelle existieren oder konstruiert werden können, welche ebenfalls auf der Chaostheorie basieren und im Hinblick auf die Zielsetzung von [Kreutzberg, 1998] wertvolle Beiträge liefern. Deshalb wird in der vorliegenden Arbeit das formale Strommodell als ein mögliches Beispiel einer Anwendung der Chaostheorie verstanden und analysiert. Die Chaostheorie wird dabei nur insoweit behandelt, wie sie sich im Strommodell und insbesondere in den eingeführten Gleichungen konkret manifestiert. Die gemachten Annahmen, Schlussfolgerungen, Grenzen und gefundenen Ergebnisse beziehen sich deshalb immer auf das Modell von [Kreutzberg, 1998]. Es ist jedoch zu beachten, dass die Grenzen des Strommodells nicht notwendigerweise auch für die Chaostheorie und nichtlinearen Modelle im allgemeinen Falle gelten.
Quoten
Die Fachabteilungs-, Informatik- und Erfahrungspool-Quoten sind im formalen Strommodell von zentralster Bedeutung. Diese Kerngrössen sind die einzigen endogenen Variablen und müssen deshalb den Ausgangspunkt bei der Ableitung von Ergebnissen und Erkenntnissen über die Realität bilden.
[Kreuzberg, 1998] definiert die Variablen (Ft, It, Et) als Quoten des betreffenden Pols am Gesamtumsatz zu einem gegebenen Zeitpunkt. Die Werte der Variablen liegen zwischen null und eins.
Aufgrund der Definition und der Verwendung der Quoten im formalen Strommodell ist die Abgrenzung nicht eindeutig, und es bleibt ein Interpretationsspielraum. Insbesondere sieht das Strommodell keinen "Mechanismus" vor, damit die Summe aller Quoten kleiner oder gleich eins ist. Die Summe kann eins übersteigen.
Im folgenden werden deshalb diese wichtigen Grössen analysiert, interpretiert und schliesslich definiert. Annahmen, Einschränkungen und Schwierigkeiten werden beschrieben. Bei den Ausführungen wird auf die anfallenden Kosten und Umsätze der einzelnen Abteilungen eingegangen. Der Einfachheit halber wird dabei so getan, als ob die betreffenden Abteilungen die Kalkulation selbst durchführen. Wird beispielsweise geschrieben, dass die Informatikabteilung der Fachabteilung 60 Geldeinheiten verrechnet, dann kann dies gleichgesetzt werden mit der Aussage, dass das betriebliche Rechnungswesen für die Leistungen der Informatikabteilung 60 Geldeinheiten kalkuliert und der Fachabteilung belastet hat.
Der Umsatz stellt die Bezugsgrösse zu den Quoten dar. [Gabler, 1997] definiert den Umsatz als "Summe der in einer Periode verkauften, mit ihren jeweiligen Verkaufspreisen bewerteten Leistungen".
Eine Schwierigkeit ergibt sich dabei aus der Tatsache, dass die erstellten Leistungen von der zuständigen Instanz mit dem Verkaufspreis bewertet werden. Diese Bewertung stützt sich nicht zwangsläufig auf die Selbstkosten der Produkte ab, und selbst bei den Kosten lässt sich eine "absolut" objektive Bewertung kaum realisieren. Es liegt also im Ermessen der betreffenden Instanz, wie sich die Preise ergeben, welche anschliessend den Umsatz bestimmen. Möchte das Unternehmen ein neues Produkt einführen und mittels Tiefpreisen Kunden gewinnen, so wird der Verkaufspreis nahe bei den Selbstkosten und im Extremfall sogar darunter liegen. Umgekehrt kann beispielsweise bei einer "Cash Cow" und der damit verbundenen Abschöpfungsstrategie die Differenz zwischen den Selbstkosten und den Verkaufspreisen sehr hoch ausfallen. Ein konstantes Verhältnis zwischen Kosten und Verkaufspreisen resultiert nicht. Die Verkaufspreise werden subjektiv und von Fall zu Fall unterschiedlich festgelegt. Zudem kann aufgrund des Umsatzes nicht auf die Kosten und schliesslich auf die Gewinne geschlossen werden.
Die Unternehmung erstellt durch Kombination ihrer Produktionsfaktoren Erzeugnisse (Leistungen). Der betriebliche Umsatzprozess "Input ® Transformation ® Output" ergibt sich ebenfalls - auf einer tieferen Ebene - für die einzelnen Abteilungen. So kombiniert die Informatikabteilung ihre Ressourcen, um beispielsweise Leistungen für die Fachabteilung zu erbringen; es kann somit vom Umsatz einer Abteilung gesprochen werden. Typischerweise wird die Informatikabteilung den anderen Abteilungen Dienstleistungen verkaufen. Die erbrachten Leistungen der Informatikabteilung dienen den anderen Einheiten dazu, selbst die geforderte Leistung zu erbringen, so dass schlussendlich ein Endprodukt resultiert. Das Endprodukt wird an den Kunden verkauft, und der Preis fliesst in den Unternehmensumsatz ein. Bezüglich des Strommodells ergibt sich nun die Frage, auf welchen Umsatz sich beispielsweise die Quote der Informatikabteilung bezieht. Würden beispielsweise nur diejenigen Abteilungen betrachtet werden, welche die Endprodukte verkauft haben, dann hätte die Informatik- und Erfahrungspoolquote einen Wert von null; diese beiden Einheiten unterstützen ja "nur" die anderen Abteilungen und verkaufen selbst keine Endprodukte. Selbstverständlich ist eine solche Betrachtungsweise zu kurzsichtig, da sowohl Erfahrungspool als auch Informatikabteilung normalerweise einen wertvollen Beitrag an die anderen Abteilungen und somit indirekt auch ans Endprodukt liefern. Die objektive Bemessung dieses Anteils ist allerdings mit erheblichen Schwierigkeiten verbunden. Wieviel trägt beispielsweise das Mailsystem in der Fachabteilung zum Umsatz bei? Aus diesem Grund wird sich ein objektiver Anteil der Informatikabteilung am Umsatz der Fachabteilung beziehungsweise ein objektiver Anteil des Erfahrungspools am Umsatz der Informatikabteilung kaum berechnen lassen.
In einem anderen Lösungsansatz kann die Summe der verrechneten Preise für die Leistungen der Informatikabteilung an die Fachabteilung ins Verhältnis zum Gesamtumsatz der Informatikabteilung gesetzt werden. Dabei ist allerdings zu beachten, dass sich die Umsatzgewinnrate der Informatikabteilung grundlegend von den Gewinnraten der anderen Abteilungen unterscheiden kann, weil es sich unter anderem um unterschiedliche Kunden handelt (intern und extern). Weiter ist bei einer solchen Betrachtungsweise zu berücksichtigen, dass eine Quote kleiner als eins einen zusätzlichen, versteckten Pol impliziert. Eine Informatikquote kleiner als eins bedeutet, dass die Informatikabteilung nicht ausschliesslich für die Fachabteilung arbeitet, sondern für den Erfahrungspool und weitere, versteckte Einheiten Leistungen erbringt. Wieviel dabei für eine versteckte Einheit (unter mehreren) "abgezweigt" wird, ist mangels Kenntnis der anderen Quoten und Einheiten nicht bekannt.
Die bisherigen Ausführungen zeigen, dass die Höhe der Verkaufspreise, welche schliesslich in den Umsatz einfliessen, "subjektivere" Grössen sind als die Kosten. Zudem ist die objektive Bemessung des Anteils der Abteilungen am Gesamtumsatz äusserst schwierig, und Betrachtungen der einzelnen Abteilungsumsätze sind ebenfalls mit Problemen behaftet. Weiter kann aufgrund des Umsatzes nicht auf die Kosten geschlossen werden, da nur in Ausnahmefällen von einer konstanten Gewinnrate ausgegangen werden kann.
Aufgrund der bisherigen Überlegungen zeigt sich, dass der "Umsatz" als Bezugsgrösse gewisse Schwächen aufweist.
Einschränkungen können aufgehoben werden, wenn als Bezugsgrösse der Quoten die Gewinne verwendet werden. Produktivität und Wirtschaftlichkeit berücksichtigen ebenfalls sowohl "Input" als auch "Output". Eine solche Interpretation der Quoten ist jedoch mit erheblichen Schwierigkeiten bei der Anwendung im Strommodell verbunden. Die Quoten müssen zwischen null und eins liegen, und im Falle von negativen Gewinnen (Verlusten) ändert die Bedeutung der Höhe der Quote grundlegend.
Die Bezugsgrösse "Selbstkosten der Produkte" weist Ähnlichkeiten zur Grösse "Umsatz" aus, berücksichtigt aber wiederum die andere Seite der Medaille - die Erträge - nicht. Dies ist eine starke Einschränkung und erschwert insbesondere die Ableitung von Erkenntnissen. Die Selbstkosten weisen aber gegenüber den "Verkaufspreisen (® Umsatz)" den Vorteil auf, dass sich in den entsprechenden Werten nicht die subjektive Preisbildung niederschlägt. Es stellt sich aber auch bei diesem Ansatz die Frage, auf welche Kosten sich die Quoten genau beziehen.
Weiter ist es durchaus denkbar, dass Verkaufspreise mit Kosten in Beziehung gesetzt werden. Wird beispielsweise die Informatikabteilung aus dem Unternehmen ausgelagert, dann können sich für die Fachabteilung andere Kosten für bezogene Informatikleistungen ergeben als im Falle der internen Verrechnung. Normalerweise kennt die Fachabteilung in diesem Fall die Selbstkosten der bezogenen Leistung überhaupt nicht und wird mit dem Verkaufspreis konfrontiert.
Abbildung 9 illustriert ein mögliches Szenario für eine Unternehmung und deren internes Beziehungsgeflecht. Es werden fiktive Umsatzzahlen, Gesamtkosten, Preise und Selbstkosten der Produkte angenommen. Tabelle 6 orientiert sich an diesem Zahlenbeispiel und zeigt mögliche Interpretationen der Quoten. Tabelle 7 kommentiert die verschiedenen Varianten und beschreibt die jeweiligen Problembereiche und Möglichkeiten.
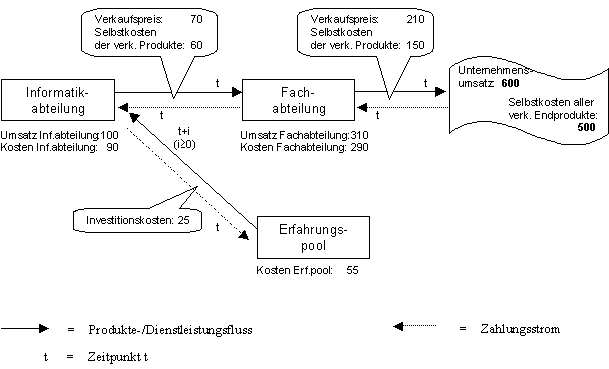
Abbildung 9: Zahlenbeispiel zu den Quoten; Szenario 1
|
a) |
Ft = 150/500 = 0.30 |
It = 60/150 = 0.40 |
Et = 25/60 = 0.42 |
|
b) |
Ft = 210/600 = 0.35 |
It = 70/210 = 0.40 |
Et = 25/70 = 0.36 |
|
c) |
Ft = 210/600 = 0.35 |
It = 70/600 = 0.12 |
Et = 25/600 = 0.04 |
|
d) |
Ft = 150/500 = 0.30 |
It = 60/500 = 0.12 |
Et = 25/500 = 0.05 |
|
e) |
Ft = 150/290 = 0.52 |
It = 60/90 = 0.67 |
Et = 25/55 = 0.45 |
|
f) |
Ft = 210/310 = 0.68 |
It = 70/100 = 0.70 |
Et = 25/55 = 0.45 |
|
g) |
Ft = 310/600 = 0.52 |
It = 100/310 = 0.32 |
Et = 55/100 = 0.55 |
|
h) |
Ft = 290/500 = 0.58 |
It = 90/290 = 0.31 |
Et = 55/90 = 0.61 |
|
i) |
Ft = 310/600 = 0.52 |
It = 100/600 = 0.17 |
Et = 55/600 = 0.09 |
|
j) |
Ft = 290/500 = 0.58 |
It = 90/500 = 0.18 |
Et = 55/500 = 0.11 |
Tabelle 6: Beispiele möglicher Interpretationen von Quoten
Im Zahlenbeispiel unterscheiden sich die Gesamtumsätze (bzw. Gesamtkosten) der jeweiligen Einheiten von der Summe der Verkaufspreise (resp. Selbstkosten). Bei einer solchen Abweichung wird davon ausgegangen, dass die einzelnen Abteilungen nicht ausschliesslich für die eingezeichneten Einheiten Leistungen erbringen. Beispielsweise betragen die Gesamtkosten der Fachabteilung "290 Geldeinheiten", während sich die Kosten der Fachabteilung bezüglich der verkauften Produkte auf "150 Geldeinheiten" belaufen. Die Differenz von "140 Geldeinheiten" ist somit nicht den verkauften Produkten anzulasten; beispielsweise könnte die Fachabteilung für einen versteckten Pol Leistungen erbringen oder in die Schulung der Mitarbeiter investieren.
Weiter gilt es dabei zu beachten, dass eine klare Abgrenzung der Verkaufspreise und Selbstkosten im Hinblick auf ihren Verwendungszweck notwendig ist: Beispielsweise beziehen sich die Verkaufspreise der Informatikabteilung (70 GE) ausschliesslich auf diejenigen Produkte, welche von der Fachabteilung für die Erstellung des abgebildeten Leistungsfluss (210 GE) benötigt werden. Praktisch wird eine solche Abgrenzung kaum durchführbar sein, da die Dienstleistungen der Informatikabteilung an die Fachabteilung sich nicht auf Produkt (-paletten) auftrennen lassen werden.
Um diese Probleme zu lösen, drängt es sich auf, dass solche "Schatteneffekte" - Leistungserstellung für versteckte Pole - ausgeschlossen werden. Dies würde bedeuten, dass der Gesamtumsatz (bzw. die Gesamtkosten) der Abteilungen der Summe der eingezeichneten Verkaufspreise (resp. Selbstkosten der verkauften Produkte) entspricht. Im Beispiel wäre der Gesamtumsatz der Fachabteilung somit "210 GE". Ausnahme bildet die Informatikabteilung im Zusammenhang mit dem Erfahrungspool, welcher gemäss Definition solches zukünftige Leistungspotential sammelt.
Der Vollständigkeit wegen werden die Schatteneffekte in der Tabelle 7 ebenfalls beschrieben, dann im weiteren Verlauf der Arbeit aber ausgeschlossen. Beim Erfahrungspool kann sich der Zeitpunkt der Investition vom Zeitpunkt des Bezugs der Leistung unterscheiden.
|
Kommentar zu den Quotenbeispielen
|
||
|
Variante |
Berechnung / Bedeutung |
Bemerkungen / Kritik |
|
a) |
Ft: Die Selbstkosten der Produkte, welche die Fachabteilung verkauft hat und welche direkt in den Unternehmensumsatz einfliessen, werden in Beziehung zu den Gesamtkosten aller verkauften Endprodukte gesetzt. It: Die Selbstkosten der Leistungen, welche die Informatikabteilung für die Fachabteilung erbracht hat, werden ins Verhältnis zu den Selbstkosten derjenigen Produkte gesetzt, welche die Fachabteilung verkauft hat und welche direkt in den Unternehmensumsatz einfliessen. Et: Die Investitionskosten der Informatikabteilung in den Erfahrungspool werden in Beziehung zu denjenigen Kosten der Informatikabteilung gesetzt, welche für die Leistungserstellung an die Fachabteilung angefallen sind.
|
|
|
b) |
Ft: Der Umsatz der Fachabteilung für Endprodukte wird ins Verhältnis zum Unternehmensumsatz gesetzt. It: Die Summe der Verkaufspreise für die erbrachten Leistungen der Informatikabteilung an die Fachabteilung wird in Beziehung gesetzt zur Summe der Verkaufspreise der Endprodukte der Fachabteilung. Et: Die Investitionskosten der Informatikabteilung in den Erfahrungspool werden in Beziehung zum Preis gesetzt, welcher die Informatikabteilung von der Fachabteilung fordert.
|
|
|
c)
|
Ft: Der Umsatz der Fachabteilung für Endprodukte wird ins Verhältnis zum Unternehmensumsatz gesetzt. It: Die Summe der Verkaufspreise für die erbrachten Leistungen der Informatikabteilung an die Fachabteilung wird in Beziehung zum Unternehmensumsatz gesetzt. Et: Die Investitionskosten in den Erfahrungspool werden in Verhältnis zum Unternehmensumsatz gesetzt.
|
|
|
d)
|
Ft: Die Fachabteilungsquote wird als relativer Anteil der Kosten der Fachabteilung für Endprodukte an den Gesamtkosten aller verkauften Endprodukte definiert. It: Die Informatikabteilungsquote wird als relativer Anteil der Kosten der Informatikabteilung (für Leistungen an die Fachabteilung) an den Gesamtkosten aller verkauften Endprodukte definiert. Et: Die Erfahrungspoolquote wird als relativer Anteil der Investitionskosten (der Informatikabteilung in den Erfahrungspool) an den Gesamtkosten aller verkauften Endprodukte definiert.
|
|
|
e)
|
Ft: Die Fachabteilungsquote stellt den relativen Anteil der Kosten für die Endprodukte (der Fachabteilung) an den Gesamtkosten der Fachabteilung dar. It: Die Informatikabteilungsquote stellt den relativen Anteil der Kosten der erbrachten Leistungen (für die Fachabteilung) an den Gesamtkosten der Informatikabteilung dar. Et: Die Erfahrungspoolquote wird definiert als relativer Anteil der Investitionskosten der Informatikabteilung (in den Erfahrungspool) an den gesamten Investitionskosten in den Erfahrungspool.
|
|
|
f)
|
Ft: Die Summe der Preise der verkauften Endprodukte (der Fachabteilung) wird ins Verhältnis zum Gesamtumsatz der Fachabteilung gesetzt. It: Der verrechnete Preis für die erbrachten Leistungen der Informatikabteilung für die Fachabteilung wird in Beziehung gebracht mit dem Gesamtumsatz der Informatikabteilung. Et: Die Erfahrungspoolquote wird definiert als relativer Anteil der Investitionskosten der Informatikabteilung (in den Erfahrungspool) an den gesamten Investitionskosten in den Erfahrungspool.
|
|
|
g)
|
Ft: Die Fachabteilungsquote wird definiert als relativer Anteil des Umsatzes der Fachabteilung am Unternehmensumsatz. It: Die Informatikabteilungsquote wird definiert als relativer Anteil des Umsatzes der Informatikabteilung am Umsatz der Fachabteilung. Et: Die Erfahrungspoolquote stellt den relativen Anteil der Gesamtkosten des Erfahrungspools am Umsatz der Informatikabteilung dar.
|
|
|
h) |
Ft: Die Gesamtkosten der Fachabteilung werden in Beziehung zu den Gesamtkosten aller verkauften Produkte gestellt. It: Die Gesamtkosten der Informatikabteilung werden in Beziehung zu den Gesamtkosten der Fachabteilung gesetzt. Et: Die Gesamtkosten des Erfahrungspools werden in Beziehung mit den Gesamtkosten der Informatikabteilung gesetzt.
|
|
|
i) |
Ft: Der Gesamtumsatz der Fachabteilung wird ins Verhältnis zum Unternehmensumsatz gesetzt. It: Der Gesamtumsatz der Informatikabteilung wird ins Verhältnis zum Unternehmensumsatz gesetzt. Et: Die Investitionskosten des Erfahrungspools werden in Beziehung mit dem Unternehmensumsatz gesetzt.
|
|
|
j) |
Ft: Die Fachabteilungsquote wird definiert als der relative Anteil der Fachabteilungskosten an den Gesamtkosten aller verkauften Produkte. It: Die Informatikabteilungsquote wird definiert als der relative Anteil der Informatikabteilungskosten an den Gesamtkosten aller verkauften Produkte. Et: Die Erfahrungspoolquote wird definiert als der relative Anteil der gesamten Investitionen in den Erfahrungspool an den Gesamtkosten aller verkauften Produkte.
|
|
Tabelle 7: Kommentar zu den Quotenbeispielen
Weitere Interpretationsmöglichkeiten ergeben sich, wenn beim Erfahrungspool zwischen Verkaufspreis und Kosten unterschieden wird. Falls beispielsweise das Wissen eines externen Beraters hinzugezogen wird, ist lediglich der geforderte Preis für seine Dienstleistung (indirekt für sein Wissen) bekannt. Die zeitliche Verzögerung zwischen Investitions- und Bezugszeitpunkt bleibt für die Informatikabteilung in diesem Fall aus (dafür investiert der Berater zu einem anderen Zeitpunkt in sein Wissen).
Beim Bezug von Leistungen aus dem Erfahrungspool stellt sich das Problem, wie teuer (® Verkaufspreis) dieser Leistungsbezug sein soll. Ein objektiver Betrag wird sich bereits deshalb nicht ermitteln lassen, weil nach dem Bezug der Leistungen das Wissen immer noch vorhanden ist und weiter zur Verfügung steht. Diese Tatsache ist ein weiteres Argument für die Verwendung von Investitionskosten.
Die obigen Ausführungen zeigen, dass in [Kreutzberg, 1998] die Quoten zuwenig präzise definiert sind und Interpretationsspielräume bestehen. Aufbauend auf den obigen Überlegungen wird deshalb im folgenden eine Definition vorgestellt, welche zusätzliche Annahmen fordert und dafür den Interpretationsspielraum einengt.
Die Tabelle 7 zeigt auf, dass bei jeder Variante erhebliche Probleme auftreten, wenn nebst den eingezeichneten Leistungs- und Zahlungsströmen noch weitere, versteckte Zu- oder Abflüsse existieren. Es drängt sich deshalb auf, solche Schatteneffekte auszuschliessen. Dies bedeutet aber wiederum, dass massive Einschränkungen und Annahmen gemacht werden müssen.
Neben der Beseitigung der Schatteneffekte wird zudem - wie einleitend bereits angekündigt - die Bezugsgrösse "Kosten" anstelle der Umsätze eingeführt; durch diesen Wechsel ergeben sich einige Vorteile, während die damit neu hinzugekommenen Nachteile minimal sind.
Definition:
Zusätzliche Annahmen:
Abbildung 10 illustriert anhand eines Zahlenbeispiels, wie sich die jeweiligen Kosten zusammensetzen und sich die Quoten berechnen lassen:
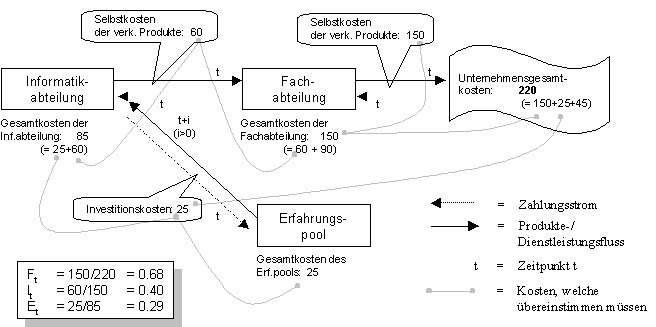
Abbildung 10: Zahlenbeispiel zu den Quoten; Szenario 2
Die erarbeitete Lösung kann mit den grundlegenden Bedingungen, welche [Kreutzberg, 1998] fürs formale Strommodell fordert, vereinbart werden; es entstehen keine Widersprüche. Erkauft wird sich diese Lösung, indem zusätzliche Einschränkungen gemacht werden müssen. Insbesondere fliessen sehr tiefgreifende Annahmen ins Modell ein, wenn gefordert wird, dass die Fachabteilung für keine andere Einheit des Unternehmens Leistungen erbringen und auch nicht in ihr künftiges Leistungspotential investieren darf.
Entspricht die Höhe der Unternehmensgesamtkosten nicht der Summe der Kosten der Fachabteilung und Investitionskosten in den Erfahrungspool, so wird implizit von einem weiteren, versteckten Pol ausgegangen: Dieser "Schattenpol" trägt in diesem Fall ebenfalls zu den Gesamtkosten bei, und die zusätzlichen Annahmen fordern, dass weder die Informatik- noch die Fachabteilung für diesen Pol Leistungen erbringen dürfen. Der Pol kann nur beseitigt werden, wenn unter dem Begriff "Fachabteilung" sämtliche Abteilungen der Unternehmung - mit Ausnahme der Informatikabteilung - zusammengefasst werden. Durch den Ausschluss solcher "kostenverursachenden" Schattenpole aus dem Modell verliert aber wiederum die Fachabteilungsquote an Bedeutung; bei dieser Interpretation des Begriffs "Fachabteilung" nimmt die betreffende Quote sehr hohe Werte an. (Eine Quote von eins wird nur deshalb nicht erreicht, weil die Investitionskosten für den Erfahrungspool in den Unternehmensgesamtkosten enthalten sind, aber nicht in den Fachabteilungskosten. Wenn die Informatikabteilung nicht in den Erfahrungspool investiert, ergibt sich bei dieser Interpretation immer eine Fachabteilungsquote von eins.)
Wie weiter oben bereits beschrieben, weist die neu vorgeschlagene Bezugsgrösse "Kosten" zur Berechnung der Quote gegenüber der Grösse "Umsatz" Vorteile auf. Es gilt aber zu beachten, dass die Bezugsgrösse "Kosten" (gleich wie der Umsatz) nur eine beschränkte Aussagekraft hat, weil die andere Seite der Medaille - die Ertragsseite (bzw. die Kostenseite) - nicht berücksichtigt wird. Wenn nicht beide Seiten betrachtet werden, sind insbesondere Prognosen dieser Grössen über die Zeit sehr kritisch zu beurteilen.
Im weiteren Verlauf der Arbeit wird auf der vorgestellten Definition und den Zusatzannahmen (in Absprache und Übereinstimmung mit Kreutzberg) aufgebaut.
Im formalen Strommodell fliesst die exogene Variable Ut ein. Da neu die Bezugsgrösse "Kosten" verwendet wird, drängt es sich auf, dass die Gesamtkostenwachstumsrate anstelle der Umsatzwachstumsrate verwendet wird. Die Gesamtkostenwachstumsrate wird mit "Kt" abgekürzt und ist als das Verhältnis "Kosten im Zeitpunkt 't' minus Kosten im Zeitpunkt 't-1'" zu "Kosten im Zeitpunkt 't'" definiert.
Kausalitätsstruktur
Das formale Strommodell setzt sich aus drei Stufen zusammen. In den betreffenden drei Gleichungen wird der funktionale Zusammenhang der Parameter und Variablen definiert. Die Elemente werden nun in einem Blockdiagramm in Beziehung gesetzt, um das Verhältnis zwischen Ursachen und Wirkungen gesamthaft darzustellen. Die Kausalitätsstruktur des Modells wird dadurch übersichtlich abgebildet; Grenzen und Möglichkeiten der gegenseitigen Einflüsse werden erkennbar.
Im Blockdiagramm sind sämtliche Variablen und Parameter aus dem formalen Strommodell (erster bis dritter Stufe) übernommen worden. Diese Elemente werden mit Pfeilen in der Richtung verbunden, wie sie sich beeinflussen. Es resultiert ein Diagramm, wie es in Abbildung 11 gezeichnet ist:
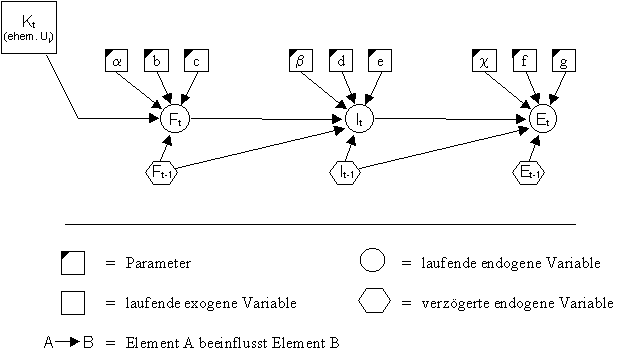
Abbildung 11: Blockdiagramm des formalen Strommodells
Eine triviale, aber sehr weitreichende Feststellung betrifft die Gesamtkostenwachstumsrate Kt (ehemalige Umsatzwachstumsrate): Die Gesamtkosten und deren Änderung im Laufe der Zeit werden vom Modell nicht erklärt. Aus diesem Grund kann bei Erklärungsversuchen zur Entwicklung der Unternehmung diese Grösse nicht als Indikator herangezogen werden. Das Diagramm veranschaulicht zudem, dass Kt die einzige exogene Variable im Zeitpunkt t ist.
In versteckter Form fliessen drei weitere, von aussen vorgegebene Variablen ins Modell ein: die Startwerte F0, I0 und E0. Sie sind lediglich im Falle eines eindeutigen, stabilen Gleichgewichts sämtlicher Startwerte uninteressant.
Auffällig sind die zahlreichen Parameter, welche per Definition ebenfalls exogene Grössen darstellen. Das formale Strommodell kann in diesem Sinne als sehr offenes Modell bezeichnet werden, was von [Kreutzberg, 1998] explizit als ein Ziel erklärt wird. Es gilt weiter zu beachten, dass der Übergang vom Parameter zur Variablen fliessend sein kann. So könnte beispielsweise im Strommodell der Parameter a als exogene Variable definiert werden, welche sich im Laufe der Zeit verändert; denkbar wäre auch eine endogene Variable a , welche sich proportional zum Kostenwachstum verhält. Beim Strommodell sollte im Falle einer "Umwandlung" vom Parameter zur Variablen insbesondere berücksichtigt werden, dass sämtliche Variablen vom Faktor Zeit abhängen. Somit sollten neu eingeführte Variablen diesem Design Rechnung tragen. Insofern ist der Übergang doch etwas grösser als es der erste Blick vermuten lässt.
Zentrale Grössen im Modell sind die einzelnen Quoten, während die Parameter via Wachstums- und Dämpfungseffekt diese Variablen "steuern". Bei einer Überprüfung der Modellannahmen stellt sich deshalb die Frage, ob die Abhängigkeiten zwischen den einzelnen Variablen gerechtfertigt sind:
Ins Strommodell fliesst die Annahme, dass die Gesamtkostenwachstumsrate sich sofort auf die Fachabteilungsquote auswirkt; bei veränderlichen Gesamtkosten soll sich der prozentuale Anteil der Fachabteilung verändern. In der Regel werden die Gesamtkosten und damit auch die Veränderung derselben nicht ausschliesslich von der Fachabteilung bestimmt. Es besteht lediglich für den Fall, dass jeder Pol immer einen konstanten Anteil an den Gesamtkosten aufweist, keine Beziehung zwischen der Kostenwachstumsrate und der Fachabteilungsquote. (Zu beachten ist, dass in der Argumentation von einem Einfluss der Fachabteilung auf die Gesamtkosten ausgegangen wird; d.h., dass die umgekehrte Richtung eingeschlagen wird).
Im Modell übt die Veränderung der Fachabteilungsquote einen Einfluss auf die Quote der Informatikabteilung aus. Dieser Zusammenhang ergibt sich, wenn die Fachabteilung in ihrem Leistungserstellungs-Prozess keinen proportionalen Leistungsanteil (als Kosten bewertet) von der Informatikabteilung bezieht.
Die Änderung der Informatikabteilungsquote wirkt sich im Modell auf die Quote des Erfahrungspools aus. Sofern die Informatikabteilung ihre Investitionen in künftiges Leistungspotential nicht in ein konstantes Verhältnis zu den Kosten der geforderten Leistungen setzt, ergibt sich der betreffende Sachverhalt. Es ist davon auszugehen, dass die Informatikabteilung (bzw. die dafür zuständigen Personen) bei hohem Auftragsvolumen weniger in Aus- und Weiterbildung investieren als in Zeiten mit Überkapazitäten.
Zur Berechnung des aktuellen Werts einer Quote wird jeweils der Werte der Vorperiode berücksichtigt. Dieser Zusammenhang ist aufgrund der einfachen Tatsache plausibel, weil die Vergangenheit sicherlich die gegenwärtige Ausprägung der jeweiligen Abteilung beeinflusst.
Somit sprechen Argumente für die Abhängigkeiten, wie sie im formalen Modell abgebildet werden.
Sehr deutlich kommt in der Abbildung 11 zum Ausdruck, dass im formalen Strommodell keine Schleifen und Wechselwirkungen zwischen den Elementen auftreten. Insbesondere übt die Erfahrungspoolquote im Modell keinen Einfluss auf die Informatik- und Fachabteilungsquote aus. Ebenso hat die Informatikabteilungsquote keinerlei Auswirkungen auf die Fachabteilungsquote. Ursache und Wirkung bewegen sich stets entlang einer "Linie".
Das Blockdiagramm in Abbildung 11 stellt die Beziehungen zwischen den Elementen dar, wie sie im Strommodell definiert wurden. Daneben sind - wie im vorherigen Abschnitt angedeutet - weitere Abhängigkeiten dieser Elemente denkbar. In Tabelle 8 werden deshalb Beispiele für zusätzliche, mögliche Einflussfaktoren auf die vorhandenen Variablen und Parameter vorgestellt. Zudem wird nochmals die Bedeutung der einzelnen Elemente hervorgehoben.
Aufgrund der Komplexität der Realität sowie der steigenden Schwierigkeiten bei Hinzunahme weiterer Aspekte ins Modell ist ein geeignetes Abstraktionsniveau zu finden. In diesem Sinne können die Vorschläge aus Tabelle 8 höchstens vereinzelt als Erweiterungen ins Modell einfliessen. Primär dient die Aufzählung dem Zweck, Grenzen und Erweiterungsmöglichkeiten des Strommodells aufzuzeigen.
|
Abkürzung |
Bedeutung des Elements |
Wovon ist dieses Element im Modell abhängig? |
Welche Einflussgrössen auf das Element sind denkbar, sind aber im formalen Modell nicht enthalten? |
Bemerkungen |
|
Kt (Ut) |
Gesamtkosten-wachstumsrate (Umsatzwachs-tumsrate) |
Exogene Variable; Element wird durch das Modell nicht erklärt.
|
Erfahrungspoolquote, Fachabteilungsquote, Informatikabteilungsquote, allgemeine Marktlage (Konjunktur), Art des Produkts, Unternehmensgrösse, Branchenentwicklung, Marktpotential und -anteil, Kosten aus früheren Perioden
|
|
|
a |
Beeinflussung des Wachstums der Fachabteilungs-quote
|
Parameter; d.h. konstante exogene Grösse, welche vom Modell nicht erklärt wird.
|
b , c , allgemeines Unternehmenswachstum, Wachstum der anderen Abteilungen, Branchenwachstum, Erfahrungspoolquote
|
Kt hat zwar nicht via a , dafür über Umwege einen Einfluss auf die massgebende Zielgrösse Ft.
|
|
b , c |
Einflussfaktor auf das Wachstum der Informatikab-teilungs- bzw. Erfahrungspool-quote
|
Parameter |
vgl. Aufzählung bei "a " (sinngemäss übersetzt) |
vgl. Bemerkungen bei "a " (sinngemäss übersetzt) |
|
b |
Einflussfaktor auf den Dämpfungseffekt der Fachabteilungs-quote
|
Parameter |
d, f, Komplexität der Aufgabe, It, Et |
Es ist denkbar, dass die Intensität des Dämpfungseffekts von den Quoten der anderen Einheiten abhängig ist (dieser Aspekt könnte via "b" aufgenommen werden).
|
|
d, f |
Einflussfaktor auf den Dämpfungseffekt der Informatikabteilungs- bzw. Erfahrungspool-Quote
|
Parameter |
vgl. Aufzählung bei "b" (sinngemäss übersetzt) |
vgl. Bemerkungen bei "b" (sinngemäss übersetzt) |
|
c |
Dieses Element bestimmt die Höhe des Dämpfungseffekts der Fachabteilungs-quote in Verbindung mit der Kostenwachs-tumsrate. |
Parameter |
Unternehmensstrategie, Art des Produktes und der Aufgabe |
Wenn beispielsweise bei hohen Umsätzen und Gesamtkosten eine Diversifikationsstrategie verfolgt wird, sollte der absolute Wert von c hoch sein. (Neue Einheiten vermindern ceteris paribus die Quoten der anderen Abteilungen.)
|
|
e, g |
vgl. mit Bedeutung von c. (sinngemäss)
|
Parameter |
vgl. mit Aufzählung von c. |
vgl. mit Bemerkungen von c. |
|
Ft |
Fachabteilungs-quote |
Kt, Ft-1, a , b, c |
Informatikabteilungsquoten zu verschiedenen Zeitpunkten, Erfahrungspoolquoten zu verschiedenen Zeitpunkten, Höhe der Kosten in der Vergangenheit (direkter Einfluss), Quoten von versteckten Einheiten im Unternehmen (Bsp. Unternehmensleitung), Art des Produktes und der Aufgabe (® Branchenwerte), Arbeitseinstellung und Fähigkeiten der Mitarbeiter, Technologieentwicklung, Methoden, Techniken, Instrumente, Personaländerungen, allgemeine Wirtschaftslage
|
|
|
I t |
Informatikab-teilungsquote |
Ft, Ft-1, I t-1, b , d, e |
vgl. Aufzählungen bei Ft (sinngemäss übersetzt)
|
|
|
E t |
Erfahrungspool-quote |
I t, I t-1, E t-1, c , f, g |
vgl. Aufzählungen bei Ft (sinngemäss übersetzt)
|
Tabelle 8: Abhängigkeiten der Elemente im formalen Strommodell
Nichtlinearitätsfaktor
Eine positive Eigenschaft des formalen Strommodells ist es, dass der Faktor Zeit beachtet wird und dadurch Prozesse anstelle von statischen Situationen berücksichtigt werden. Sämtliche endogene Variablen (Ft, It, Et) sind von den jeweiligen Werten der Vorperiode abhängig. Daneben übt zusätzlich die Veränderung der Gesamtkosten beziehungsweise der Quoten einen Einfluss auf die Werte der betreffenden endogenen Variablen aus.
Abbildung 12 stellt die funktionalen Zusammenhänge und Bedingungen aus dem formalen Strommodell nochmals dar:
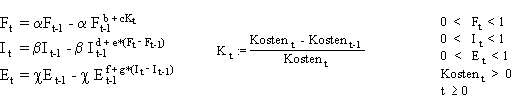
Abbildung 12: Gleichungen und Bedingungen aus dem formalen Strommodell
Wie aus Abbildung 12 ersichtlich ist, weisen die drei Gleichungen zur Berechnung der Quoten eine ähnliche Struktur auf. Die Ausdrücke "It-It-1", "Ft-Ft-1" und Kt geben dabei jeweils eine Änderung einer Grösse im Laufe der Zeit an. Aufgrund der Definition der Gesamtkostenwachstumsrate Kt und unter der Annahme, dass die Kosten immer grösser als null sind, ergibt sich die logische Folgerung, dass die Kostenwachstumsrate Kt analog zu den Quoten immer kleiner als eins ist. Es ist jedoch zu beachten, dass sich der Nichtlinearitätsfakor der Fachabteilung (b+c*Kt) im Gegensatz zu den Faktoren der anderen Abteilungen trotzdem stark unterscheidet: Während die Differenz zweier Quoten (hier: "Ft-Ft-1" und "It-It-1") immer grösser als "-1" ist, gibt es für die Werte der Kostenwachstumsrate Kt theoretisch keine untere Grenze. Wenn die Gesamtkosten der Unternehmung im Vergleich zur Vorperiode sinken, so nimmt Kt negative Werte an, wobei der absolute Betrag von eins sehr schnell überstiegen werden kann. Dieser Sachverhalt resultiert, weil die Bedeutung der Variablen in den Nichtlinearitätsfaktoren verschiedener Art sind: Zum einen handelt es sich um die Differenz zweier Quoten, zum anderen um die relative Änderung einer Grösse im Laufe der Zeit. Diesem Aspekt gilt es bei der Wahl der Parameter "b" und "c" Rechnung zu tragen.
[Kreutzberg, 1998] schliesst Nichtlinearitätsfaktoren kleiner oder gleich eins aus. Die Forderung ist gerechtfertigt, da die Quoten sonst unerlaubte Werte annehmen. Das Ergebnis ergibt sich, wenn beispielsweise in Abbildung 12 in der ersten Gleichung der Faktor "Ft-1" auf der rechten Seite vorgeklammert wird.