4.2.1 Prinzipal-Agent-Beziehungen im Strommodell
In einer Unternehmung existiert eine Vielzahl von Prinzipal-Agent-Beziehungen. So sind auch innerhalb des Strommodells mehrere solche Beziehungen denkbar: Erteilt die Fachabteilung der Informatikabteilung einen Auftrag, so übernimmt der Vertreter des Fachbereichs die Rolle des Prinzipals, während der Informatikmitarbeiter als Agent aufgefasst werden kann. Innerhalb einer Abteilung können ebenfalls entsprechende Beziehungen auftreten, wenn beispielsweise der Informatikleiter einer unterstellten Instanz einen Auftrag erteilt oder ein Informatikmitarbeiter einen Arbeitskollegen beauftragt. Der "klassische" Fall liegt vor, wenn die Aktionäre als Prinzipal und das Top-Management als Agent verstanden werden. Zwischen dem Top-Management (® Pol "Unternehmensleitung") und der Informatik- beziehungsweise Fachabteilung besteht ebenfalls eine Prinzipal-Agent-Beziehung.
Erkenntnisse aus der Prinzipal-Agent-Theorie können auf diese Beziehungen übertragen werden, wobei sich natürlich die Frage stellt, ob die betreffenden Modellannahmen mit den tatsächlichen Gegebenheiten der jeweiligen Prinzipal-Agent-Beziehungen übereinstimmen. Wie im vorhergehenden Unterkapitel beschrieben wird, existieren zahlreiche Prinzipal-Agent-Modelle, welche unterschiedliche Schwerpunkte festlegen. So wird beispielsweise bei einem Auftrag, welcher die Informatikabteilung für die Fachabteilung erfüllt, typischerweise der Wissensvorsprung der Informatikmitarbeiter gegenüber der Fachabteilung sehr gross sein, weshalb sich eine Modellierung dieser Prinzipal-Agent-Beziehung auf der Grundlage von "hidden information"-Modellen aufdrängt. Demgegenüber wird beispielsweise der Wissensvorsprung weniger gross sein, wenn ein Informatikmitarbeiter seinen Arbeitskollegen beauftragt. Beobachtet der Auftraggeber in diesem Fall die Aktion seines Kollegen nicht, so kann sich eine Modellierung aufgrund von "hidden action"-Modellen als geeignet erweisen. Je nach der Art der darzustellenden Prinzipal-Agent-Beziehung kann sich somit der eine oder andere Prinzipal-Agent-"Modelltyp" als Grundlage besser eignen.
4.2.2 Controlling und Prinzipal-Agent-Theorie
Wie im Unterkapitel "Prinzipal-Agent-Theorie" bereits festgehalten wird, besteht die allgemeine Zielsetzung der Prinzipal-Agent-Theorie in der optimalen Gestaltung der Anreizfunktion (Belohnungsfunktion). Dabei interessieren grundsätzlich zwei Fragen: Zum einen stellt sich die Frage der Bemessungsgrundlage (d.h. des Informationssystems), und zum anderen die Frage nach der Abhängigkeit der Zahlungen an den Agenten von dieser Bemessungsgrundlage, das heisst die Frage nach der zweckmässigen Wahl der Entlohnungsregeln (vgl. [Kiener, 1990; S. 28]).
[Kreutzberg, 1998] verfolgt mit dem Strommodell unter anderem das Ziel, für das Controlling - speziell für das Projektcontrolling - zu motivieren. Deshalb wird im folgenden darauf eingegangen, welchen Beitrag die Prinzipal-Agent-Theorie in diesem Zusammenhang liefern kann. Anhand eines Beispiels wird im nächsten Unterkapitel aufgezeigt, wie Prinzipal-Agent-Modelle mit dem formalen Strommodell kombiniert werden können und welche Erkenntnisse insbesondere bezüglich des Erfahrungspools mit dessen Elementen Erfahrungsdatenbank und Projektcontrolling resultieren.
[Chwolka, 1996] stellt fest, dass in der Literatur die Unternehmen oft als Vernetzung einer Vielzahl von Prinzipal-Agent-Beziehungen charakterisiert werden. Sie analysiert deshalb in ihrer Dissertation mit Hilfe agency-theoretischer Modelle die Rolle und den Wert einer Controlling-Institution. Zusammenfassend kommt sie zu folgenden Ergebnissen (vgl. [Chwolka, 1996]):
Die getroffenen Annahmen, die verwendeten Prinzipal-Agent-Modelle und die verschiedenen Herleitungen der Ergebnisse werden in [Chwolka, 1996] beschrieben (215 Seiten).
[Kah, 1994] befasst sich in seiner Dissertation mit der theoretischen Fundierung des Controllings, speziell mit den Koordinationsaufgaben des Controllings innerhalb des Führungsgesamtsystems. Auszugsweise sollen hier einige Überlegungen und Ergebnisse aus seiner Arbeit aufgezählt werden:
(vgl. [Kah, 1994])
Es existieren zahlreiche Prinzipal-Agent-Beziehungen im Unternehmen, und zu deren Modellierung stehen verschiedene " Prinzipal-Agent-Modelltypen" zur Verfügung. Zur Motivation für den Aufbau des Controllings mittels Prinzipal-Agent-Theorie gibt es verschiedene Ansatzmöglichkeiten. Typische Eigenschaft von Modellen ist die Reduktion der Komplexität. Je präziser versucht wird, den relevanten Umweltausschnitt darzustellen, desto mehr wird die Komplexität des Modells ansteigen, wodurch die logische Analyse erschwert oder sogar verunmöglicht werden kann. Insofern müssen bei einer konkreten Erweiterung des formalen Strommodells um den Prinzipal-Agent-Ansatz Einschränkungen getroffen werden; eine Prinzipal-Agent-Beziehung muss ausgewählt und auf der Grundlage eines geeigneten Prinzipal-Agent-Modelltyps dargestellt werden. Idealerweise wird das betreffende Modell verfeinert, oder es werden andere Beziehungen anhand weiterer Prinzipal-Agent-Modelle analysiert, um sich einem umfassenden Modell anzunähern. Welche Erkenntnisse dadurch für das Controlling resultieren können, zeigen beispielsweise die aufgeführten Ergebnisse von [Chwolka, 1996] und [Kah, 1994]. Im nächsten Unterkapitel wird anhand einer ausgewählten Prinzipal-Agent-Beziehung und auf der Grundlage eines speziellen Prinzipal-Agent-Modelltyps ein weiterer "Baustein" zur Fundierung des Controllings vorgestellt. Dabei wird das betreffende Prinzipal-Agent-Modell mit dem nichtlinearen Modell von [Kreutzberg, 1998] kombiniert.
4.2.3 Integration von Prinzipal-Agent-Modellen ins formale Strommodell
In den vorhergehenden Abschnitten werden Ergebnisse der Prinzipal-Agent-Theorie aufgezeigt. Diese Ergebnisse werden aufgrund von Prinzipal-Agent-Modellen abgeleitet, welche im Hinblick auf eine spezielle Fragestellung konstruiert sind, jedoch bezüglich der Wahl von Funktionen, Parametern und Variablen oft sehr allgemein behandelt werden. Eine Erkenntnis aus der Prinzipal-Agent-Theorie ist beispielsweise, dass der Agent keinen fixen Lohn erhalten sollte, wenn er risikoneutral ist (vgl. [Petersen, 1989; S. 59]). Der Vorteil solcher allgemeinen Aussagen liegt auf der Hand; es werden möglichst wenig Einschränkungen gemacht, so dass das Ergebnis für eine Vielzahl von Fällen gilt.
Wie das soeben genannte Beispiel verdeutlicht, können solche Prinzipal-Agent-Modelle nicht ins formale Strommodell integriert werden, ohne dass zusätzliche Annahmen getroffen werden. Im formalen Strommodell werden den einzelnen Elementen Werte zugewiesen (Pole werden durch Quoten repräsentiert), weshalb bei einer Integration von Prinzipal-Agent-Modellen die entsprechenden Funktionen und Parameter konkret festgelegt werden müssen. Im folgenden wird eine mögliche Erweiterung des formalen Strommodells aufgezeigt.
Die vorgestellten Prinzipal-Agent-Modelle sind in Anlehnung an Modelle von [Petersen, 1989; S. 110-135] und [Spremann, 1989; S. 17-30] konstruiert: Das Prinzipal-Agent-Modell von [Petersen, 1989] sowie dessen Ergebnisse werden direkt übernommen, und Beiträge von [Spremann, 1989] werden verwendet, um das Modell von [Petersen, 1989] auszubauen.
Bei beiden vorgestellten Prinzipal-Agent-Modellen besteht ausschliesslich asymmetrische Informationsverteilung bezüglich der Aktion des Agenten (® hidden action). Der Leiter der Informatikabteilung wird als Prinzipal und der Informatikmitarbeiter als Agent verstanden. Da der Agent normalerweise über einen längeren Zeitraum für die Unternehmung arbeitet, wird davon ausgegangen, dass dem Manager (Prinzipal) die wesentlichen Eigenschaften/Fähigkeiten des Mitarbeiters bekannt sind. Um eine zu hohe Komplexität des Modells zu vermeiden, wird deshalb angenommen, dass der Prinzipal vollständig über die Fähigkeiten des Agenten informiert ist. Zwecks Reduktion der Komplexität wird weiter vorausgesetzt, dass der Prinzipal (als Leiter der Informatikabteilung) über gleichviel Expertenwissen verfügt wie der Agent.
[Krcmar, 1997] nennt als Aufgaben des Projektcontrollings unter anderem: Ist-Datenerfassung, Projektdokumentation und Berichtgenerierung. Die daraus resultierenden Informationen sowie die Erfahrungsdatenbank kann der Manager (Prinzipal) benutzen, um die Arbeitsleistung des Agenten besser einzuschätzen. Er hat zusätzliche Informationen. Dieser Aspekt wird im folgenden in einem erweiterten Prinzipal-Agent-Modell (M+) diskutiert, wobei das betreffende Modell ins formale Strommodell integriert wird.
Grundidee
Die leitende Instanz der Informatikabteilung (der Manager) wird als Prinzipal verstanden, der Informatikmitarbeiter als Agent. Der Manager erteilt dem Agenten einen Auftrag, worauf der Agent die entsprechende Arbeit verrichtet. Der Manager profitiert vom Ergebnis, muss den Agenten jedoch für dessen Arbeitsaufwand entschädigen. Der Nutzen des Agenten bestimmt sich aus der Belohnung abzüglich des Disnutzens für die geleistete Arbeit.
Es wird nun untersucht, wie sich die Arbeitsleistung des Agenten sowie der erwartete Nutzen des Prinzipals verändern, wenn die Belohnung des Agenten von zusätzlichen Informationen über die Arbeitsleistung (Monitoring-Signal) abhängig gemacht wird: Im Standard-Prinzipal-Agent-Modell M- wird der Agent ausschliesslich aufgrund seines "Geschäftsergebnisses" belohnt. Im erweiterten Prinzipal-Agent-Modell M+ gelten die gleichen Voraussetzungen und Annahmen wie in M-, jedoch wird die Belohnung zusätzlich von weiteren Informationen über die Arbeitsleistung abhängig gemacht.
Die zusätzlichen Informationen über die Arbeitsleistung des Agenten (Monitoring-Signal) sind fehlerbehaftet. Ansonsten würde Informations-Symmetrie bestehen, womit das Prinzipal-Agent Problem einfach gelöst werden könnte. Weiter wird untersucht, welche Auswirkungen eine Veränderung der Varianz des Monitoring-Signals auf die Arbeitsleistung und den Nutzen hat.
Die "Schnittstelle" zum formalen Strommodell bildet der Erfahrungspool beziehungsweise dessen Elemente "Projektcontrolling" und "Erfahrungsdatenbank". Das Projektcontrolling sammelt Informationen über die Arbeitsleistungen des Agenten, bereitet sie auf und stellt sie dem Manager zur Verfügung. Es wird davon ausgegangen, dass Effizienz und Effektivität des Projektcontrollings einen Einfluss auf die Varianz des fehlerbehafteten Signals haben. Weiter dient die Erfahrungsdatenbank dem Manager (und dem Projektcontroller) dazu, die Arbeitsleistungen des Agenten besser einzuschätzen - oder anders formuliert, die Varianz des Monitoring-Signals zu verkleinern.
Wird die Erfahrungspoolquote als ein Mass für Effizienz und Effektivität des Erfahrungspools beziehungsweise von dessen Elementen verstanden, so kann die Varianz des Signals relativ einfach mit der Quote in Verbindung gebracht werden (z.B.: Varianz des Monitoring-Signals = - log[Erfahrungspoolquote] ). Wenn die Erfahrungspoolquote als Mass für die relative Höhe der Investitionskosten in den Pool verstanden wird (vgl. Kapitel "Quoten"), so muss zusätzlich gefordert werden, dass Investitionen in den Pool Wirkung zeigen, indem sie die Varianz des Signals in geeigneter Weise beeinflussen (hohe Kosten bewirken eine Abnahme der Varianz).
Die Prinzipal-Agent-Modelle "M -" und "M +"
Um die Veränderungen zu untersuchen, welche mit der Hinzunahme von Monitoring-Signalen resultieren, werden die beiden Prinzipal-Agent-Modelle M- und M+ eingeführt. Die beiden Modelle unterscheiden sich lediglich darin, dass ausschliesslich im Prinzipal-Agent-Modell M+ das Monitoring-Signal in der Belohnungsfunktion berücksichtigt wird.
In beiden Modellen M- und M+ gelten folgende Annahmen und Bedingungen:

Abbildung 20: Annahmen und Bedingungen der Prinzipal-Agent-Modelle M- und M+
Das Standardmodell, wie es im Kapitel "Prinzipal-Agent-Theorie" vorgestellt wird, bildet für beide Modelle die Basis. Präzisiert werden in M- und M+ insbesondere die Nutzenfunktionen des Prinzipals und des Agenten. Es handelt sich bei den entsprechenden Funktionen um CARA-Nutzenfunktionen (Constant Absolute Risk Aversion). Als Mass für die Risikoaversion wird das "Arrow-Pratt"-Mass gewählt, welches sich errechnet aus "( -(¶ 2U/¶ w2) / (¶ U/¶ w) ) = rA" beziehungsweise "( -(¶ 2G/¶ w2) / (¶ G/¶ w) ) = r" (vgl. [Petersen, 1989; 110 f.]). Die Parameter r und rA der Nutzenfunktionen messen also die Risikoaversion. Je höher der entsprechende Parameter ist, desto höher ist die Risikoaversion. CARA-Nutzenfunktionen besitzen die Eigenschaft, dass der Grenznutzen immer positiv ist und abnimmt.
Der Mindestnutzen/Reservationsnutzen des Agenten wird durch den Parameter m ausgedrückt. Zur Vereinfachung von mathematischen Berechnungen wird anstelle des Mindestnutzen ausschliesslich der Parameter u verwendet, welcher sofort aus dem Mindestnutzen abgeleitet werden kann.
Der Disnutzen, welcher dem Agenten durch die Verrichtung der Arbeit entsteht, wird durch die Funktion "V(a)=a2" ausgedrückt. "Um aufwendige Rechnungen zu vermeiden, soll V als monetäres Äquivalent des Nutzenverlustes durch die Anstrengung aufgefasst und daher direkt vom Gehalt abgezogen werden. V(a) ist daher eine monetäre Grösse" ([Petersen, 1989; S. 111]).
Der Agent wählt sein Arbeitsniveau a im Intervall [0, 1/2], wobei seine minimale Anstrengung bei "a=0" liegt. Setzt er sich 100% für das Unternehmen ein, so ist "a=1/2". Das Geschäftsergebnis ist eine normalverteilte Zufallsvariable, hängt vom Arbeitsniveau des Agenten ab, und der Erwartungswert liegt ebenfalls im Intervall [0, 1/2]. Die Belohnungsfunktion setzt sich in beiden Modellen additiv zusammen, mit mindestens einem fixen Lohnanteil und einem - vom Geschäftsergebnis abhängigen - variablen Lohnanteil.
Das Prinzipal-Agent-Modell M -
Zusätzlich zu den Annahmen und Bedingungen, wie sie im vorhergehenden Abschnitt aufgezählt sind, wird im Prinzipal-Agent-Modell M- von folgenden Voraussetzungen ausgegangen:
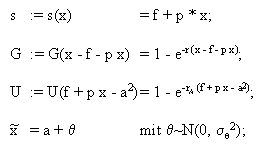
Die Belohnungsfunktion setzt sich somit aus einem fixen und variablen Teil zusammen. Der variable Lohnanteil wird ausschliesslich vom Geschäftsergebnis "x" (Output) abhängig gemacht. Dabei wird vorausgesetzt, dass das Geschäftsergebnis für beide Parteien eindeutig beobachtbar und von der Arbeitsleistung des Agenten abhängig ist. Allerdings prägen zusätzlich zur Arbeitsleistung zufällige Umwelteinflüsse das Ergebnis. Im Prinzipal-Agent-Modell M- wird davon ausgegangen, dass der Umwelteinfluss einer normalverteilten Zufallsvariable entspricht und "additiv" mit der Arbeitsleistung des Agenten auf das Geschäftsergebnis einwirkt.
Aufgrund der beschriebenen Voraussetzungen und Annahmen hat der Prinzipal im Modell M- schliesslich das folgende formale Problem zu lösen:

Als mathematische Lösung des Problems ergibt sich:
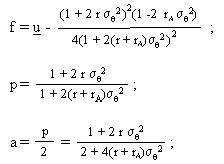
(vgl. math. Herleitung im Anhang)
Das Prinzipal-Agent-Modell M- ist eine Ausprägung eines LEN-Modells. LEN steht für (vgl. [Spremann, 1989; S. 27]):
L: Das Geschäftsergebnis ist eine lineare Funktion des Umwelteinflusses, und die Belohnungsfunktion ist eine lineare Funktion des Geschäftsergebnisses.
E: Die Nutzenfunktion U des Agenten ist eine Exponentialfunktion.
N: Der Umwelteinfluss ist eine normalverteilte Zufallsvariable.
Ein Vorteil von LEN-Modellen besteht insbesondere in deren einfachen Handhabung und Interpretierbarkeit (vgl. [Gabler, 1997]). Allerdings sind mit den LEN-Modellen die beschriebenen Einschränkungen verbunden, welche je nach Problemstellung unter Umständen nicht getroffen werden wollen.
Ein Verknüpfungspunkt des Prinzipal-Agent-Modells M- mit dem formalen Strommodell bildet die Varianz des Geschäftsergebnisses (s q ). Das Projektcontrolling und die Erfahrungsdatenbank können einen Beitrag dazu leisten, das Geschäftsergebnis des Agenten "besser" zu beurteilen und somit präziser die Arbeitsleistung des Agenten einzuschätzen. Somit kann sich der Erfahrungspool (im formalen Strommodell speziell die Quote) auf die Varianz des Geschäftsergebnisses auswirken (Et Þ s q ¯ ).
Der betreffende Zusammenhang wird jedoch nicht weiter verfolgt, da das Modell M- hier primär dem Zweck dient, den Unterschied aufzuzeigen, wenn zusätzliche Informationen über die Arbeitsleistung des Agenten erhoben werden. Die Risikoaversion des Prinzipals und des Agenten werden ebenfalls als exogene Grössen verstanden und nicht mit dem formalen Strommodell verbunden.
Das Prinzipal-Agent-Modell M +
Das Prinzipal-Agent-Modell M+ unterscheidet sich vom Modell M- lediglich darin, dass zusätzliche Informationen (nebst des Geschäftsergebnisses) gesammelt werden und diese bei der Belohnung des Agenten ebenfalls berücksichtigt werden. Für das Prinzipal-Agent-Modell M+ gelten folgende Annahmen und Bedingungen:

Der variable Anteil des Lohns hängt im Gegensatz zum Modell M- zusätzlich von weiteren Informationen über die Tätigkeit des Agenten ab (q*z), und es wird angenommen, dass die Informationen immer gesammelt werden (keine Auswertungsstrategien wie beispielsweise in [Wagenhofer, 1997; S. 425-429]).
Wie aus den oben dargestellten Bedingungen hervorgeht, wird angenommen, dass die zusätzlichen Informationen kostenlos bereitgestellt werden.
Die Informationen sind ebenfalls fehlerbehaftet, so dass es aufgrund des Monitoring Signals nicht möglich ist, mit 100 Prozent Sicherheit auf den Arbeitsaufwand des Agenten zu schliessen. Höhere Arbeitsleistungen bewirken jedoch tendenziell, dass die zusätzlichen Informationen darauf hindeuten, dass der Agent ein höheres Arbeitsniveau gewählt hat.
Analog zur Verteilung des Umwelteinflusses wird dem Zufall beim Monitoring-Signal ebenfalls mit einer normalverteilten Zufallsvariablen Rechnung getragen, welche zum Arbeitsaufwand hinzugerechnet wird. Vorausgesetzt wird im Prinzipal-Agent-Modell M+, dass die Informationen für beide Parteien eindeutig beobachtbar sind. Das Monitoring-Signal dient somit als weiterer Anhaltspunkt über die Arbeitsleistung des Agenten.
Aufgrund der genannten Voraussetzungen hat der Prinzipal im Modell M+ folgendes formale Problem zu lösen:

Als mathematische Lösung resultiert:
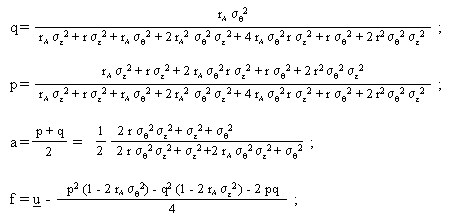
(vgl. math. Herleitung im Anhang)
Der Fixlohn f kann ebenfalls in Abhängigkeit der Parameter "r, rA, s q , s e " ausgedrückt werden. Dabei resultiert jedoch ein umfangreicher mathematischer Bruch, welcher zum allgemeinen Verständnis nicht viel beiträgt. Analog kann der Erwartungsnutzen des Prinzipals in Abhängigkeit von Risikoaversion, Mindestnutzen und Varianz der Zufallsvariablen dargestellt werden, wobei wiederum ein sehr umfangreicher mathematischer Ausdruck entsteht. Deshalb werden die entsprechenden Lösungen hier nicht aufgeführt. Bei konkreten Werten der Parameter können die betreffenden Grössen jedoch problemlos berechnet werden.
Der Nutzen des Agenten interessiert nur insoweit, als dass er mindestens gleich gross wie der geforderte Mindestnutzen sein muss. Der Prinzipal muss diesen Reservationsnutzen als konstant und vom Agenten vorgegeben betrachten und darauf aufbauend die geeignete Belohnungsfunktion festlegen. Bei genügend hohem Erwartungsnutzen des Agenten wird dieser den Arbeitsvertrag immer akzeptieren. So stellt sich schlussendlich nicht die Frage, ob der Agent den Auftrag ausführt, sondern ob aufgrund des geforderten Mindestnutzen des Agenten überhaupt noch ein positiver Erwartungsnutzen für den Prinzipal resultiert. Ist dies nicht der Fall, so wird der Prinzipal den Auftrag nicht ausführen lassen.
Zur Kombination des Prinzipal-Agent-Modells M+ mit dem formalen Strommodell werden folgende Annahmen getroffen: Der Prinzipal (Manager) erhält durch den Agenten sowie durch das Projektcontrolling und die Erfahrungsdatenbank wertvolle (zusätzliche) Informationen, um die Arbeitsleistung des Agenten präziser zu beurteilen. Der Erfahrungspool trägt somit einen wesentlichen Teil zu den zusätzlichen Informationen (Monitoring-Signal) bei. Steigt die Effizienz und Effektivität des Erfahrungspools, so kann die Arbeitsleistung des Agenten exakter beurteilt werden, weil präzisere Informationen vorliegen; die Varianz des Monitoring-Signals s e 2 nimmt ab.
Im formalen Strommodell repräsentiert die Quote den Erfahrungspool. Die Quote bezieht sich jedoch nur auf die Kosten, so dass dies nicht zwangsläufig als Massstab für die Effizienz und Effektivität des Erfahrungspools verstanden werden darf. Wird vorausgesetzt, dass hohe Investitionskosten in den Erfahrungspool Wirkung zeigen, indem die Informationen über die Arbeitsleistung präziser werden, so kann auch die Erfahrungspoolquote mit dem Monitoring-Signal "verknüpft" werden.
Abbildung 21 zeigt zwei Möglichkeiten, wie das Prinzipal-Agent-Modell M+ mit dem formalen Strommodell kombiniert werden kann:
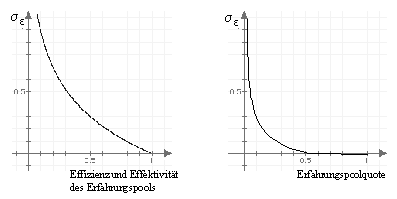
Abbildung 21: Zwei Möglichkeiten zur Verbindung des Erfahrungspools mit s e
Die beiden Beispiele aus Abbildung 21 sollen lediglich den tendenziellen Verlauf der entsprechenden Grössen wiedergeben: Mit zunehmender Effizienz/Effektivität beziehungsweise Quote des Erfahrungspools resultieren präzisere Informationen über die Arbeitsleistung des Agenten. Bei minimaler Effizienz/Effektivität beziehungsweise bei minimaler Quote können die Informationen stark fehlerbehaftet sein (Varianz ist sehr gross). Kritisch muss bei den aufgezeigten Kurvenverläufen beurteilt werden, ob eine Varianz s e 2 nahe bei null überhaupt möglich ist (® totale Überwachung). Insbesondere wird eine Steigerung von hohen Erfahrungspoolquoten kaum mehr Einfluss auf die Varianz des Monitoring-Signals ausüben.
Zur Diskussion der Ergebnisse der Prinzipal-Agent-Modelle M- und M+ sowie zu deren Kombination mit dem formalen Strommodell wird die Bezugsgrösse "Effizienz und Effektivität" des Pools verwendet. Ähnliche Ergebnisse resultieren, wenn die Erfahrungspoolquote benutzt wird; allerdings müssen dazu die genannten zusätzlichen Annahmen getroffen werden.
Erkenntnisse
Aufgrund der mathematischen Lösungen lassen sich sowohl für die Prinzipal-Agent-Modelle M- und M+ sowie deren Kombination miteinander und mit dem formalen Strommodell verschiedene Erkenntnisse gewinnen. (vgl. Anhang für die mathematischen Herleitungen)
Die Arbeitsleistung des Agenten hängt unabhängig davon, ob zusätzliche Informationen über die Arbeitsleistung bei der Belohnung berücksichtigt werden, weder vom Mindestnutzen des Agenten noch vom ausbezahlten Fixlohn ab; in den Prinzipal-Agent-Modellen M- und M+ übt sowohl der Mindestnutzen als auch der Fixlohn keinen Einfluss auf die Arbeitsleistung aus.
Die beiden Modelle M- und M+ zeigen auf, dass der Agent das tiefste aller möglichen Aktivitätsniveaus wählt, wenn er lediglich einen fixen Lohn erhält. Der Agent wird seine Arbeitsleistung nicht minimal wählen, sobald sein Lohn zusätzlich vom Geschäftsergebnis und/oder weiteren Informationen über seine Arbeitsleistung abhängig gemacht wird.
Der Provisionsanteil des Agenten aufgrund des Geschäftsergebnisses (® p) wird im optimalen Fall ebenfalls unabhängig vom Mindestnutzen des Agenten und unabhängig vom Fixlohn berechnet. Dies gilt sowohl im Modell M- als auch im Modell M+. Analoges gilt für den variablen Lohnanteil des Agenten aufgrund zusätzlicher Informationen über seine Tätigkeit (® q).
Ein Vergleich der beiden Prinzipal-Agent-Modelle M- und M+ zeigt, dass zusätzliche Informationen bezüglich der Arbeitsleistung des Agenten in dessen Belohnung berücksichtigt werden sollten (wenn eine optimale Vertragsgestaltung angestrebt wird und sofern die entsprechenden Informationen über die Arbeitsleistung des Agenten vorhanden sind).
Nimmt die Varianz des Monitoring-Signals ab (s e ¯ ), so wird der variable Lohnanteil weniger vom Geschäftsergebnis und dafür mehr von den zusätzlichen Informationen abhängig gemacht. In Verbindung mit dem Strommodell heisst dies, dass eine Steigerung der Effizienz und Effektivität des Erfahrungspools (® Projektcontrolling und Erfahrungsdatenbank) bewirkt, dass der variable Lohn des Agenten stärker von den Informationen, welcher der Pool zur Verfügung stellt, abhängig gemacht werden sollte.
Sowohl im Prinzipal-Agent-Modell M- als auch im Modell M+ ergibt sich für den optimalen Arbeitseinsatz, dass dieser steigt, wenn die Varianz des Umwelteinflusses s q 2 abnimmt. Somit steigt auch der Erwartungswert des Geschäftsergebnisses.
Wird die Arbeitsleistung im Prinzipal-Agent-Modell M+ mathematisch nach der Varianz des Monitoring-Signals abgeleitet (¶ a/¶ s e ), so resultiert unter Berücksichtigung der Modellannahmen, dass die entsprechende Ableitung immer negativ ist. Dies bedeutet, dass der Agent ein höheres Aktivitätsniveau wählt, wenn die zusätzlichen Informationen über seine Anstrengung präziser sind. Je exakter also die Informationen sind, welche der Agent und der Erfahrungspool dem Prinzipal (Manager) bereitstellen, desto höher wird der Agent sein Arbeitsniveau wählen.
Abbildung 22 zeigt diesen Sachverhalt anhand eines Beispiels grafisch auf:
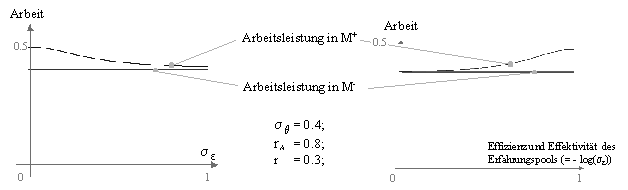
Abbildung 22: Arbeitsniveau des Agenten in M- und M+
Wie Abbildung 22 vermuten lässt, befindet sich die Arbeitsleistung im Prinzipal-Agent-Modell M+ stets auf einem höheren Niveau als im Modell M-. Dies ist auch tatsächlich der Fall, wie mit mathematischen Umformungen bewiesen werden kann.
Der Agent wählt somit immer ein höheres Arbeitsniveau, wenn zusätzliche Informationen dazu dienen, seine Leistungen zu beurteilen, und er anhand dieser Beurteilung monetär entschädigt wird. Die Belohnungsfunktion des Agenten sollte nebst des Geschäftsergebnisses von zusätzlichen Informationen abhängig gemacht werden, sofern die entsprechenden Informationen bereitgestellt werden. Projektcontrolling und Erfahrungsdatenbank können in diesem Zusammenhang wertvolle Beiträge liefern.
Der Erwartungsnutzen des Prinzipals ist im Modell M+ höher ist als in M-: Wie mathematisch gezeigt werden kann, gestaltet der Prinzipal im Modell M+ den Arbeitsvertrag derart, dass der Agent eine andere (höhere) Arbeitsleistung wählt. Somit bietet er dem Agenten im Modell M+ immer einen anderen Arbeitsvertrag an als im Modell M-, obwohl für den Prinzipal die Möglichkeit bestehen würde, auch im Modell M+ den Arbeitsvertrag aus M- zu verwenden. Weil der Prinzipal stets seinen Nutzen maximiert, wird sein Erwartungsnutzen somit höher sein, wenn der Agent zusätzlich aufgrund von weiteren Informationen variabel entlohnt wird. Um wieviel sich der Erwartungsnutzen im Modell M+ konkret gegenüber dem erwarteten Nutzen aus dem Modell M- unterscheidet, kann mit den mathematischen Lösungen, wie sie in den vorhergehenden Unterkapiteln beschrieben werden, einfach berechnet werden. Allerdings ist der absolute Wert des Nutzens wenig interessant, da er kaum interpretierbar ist. Wichtiger ist in diesem Zusammenhang die Ordnung/Reihenfolge der Werte und ob die Werte grösser als null sind.
Aufgrund zahlreicher Simulationen wird vermutet, dass der Erwartungsnutzen des Prinzipals zunimmt, wenn die Varianz des Monitoring-Signals abnimmt (s e ¯ Þ E(G) ). Wegen des enormen Umfangs wird auf den mathematischen Beweis verzichtet. Abbildung 23 veranschaulicht anhand eines Beispiels den Zusammenhang zwischen der Varianz s e 2 des Monitoring-Signals und dem Erwartungsnutzen:
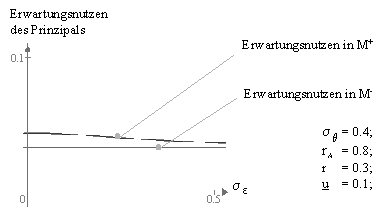
Abbildung 23: Erwartungsnutzen des Prinzipals in M- und M+
Der Erfahrungspool mit seinen Elementen Erfahrungsdatenbank und Projektcontrolling liefert zusätzliche Informationen über die Arbeitsleistung des Agenten. Werden die Informationen dazu verwendet, um die Arbeitsleistung zu beurteilen und den Agenten aufgrund dieser Informationen variabel zu entlohnen (neben einem variablen Anteil aufgrund des Geschäftsergebnisses), so steigt die Arbeitsleistung des Agenten und der Erwartungsnutzen des Prinzipals. Nimmt zudem die Effizienz und Effektivität des Erfahrungspools zu - das heisst, die Varianz des Monitoring-Signals nimmt ab - so steigt die Arbeitsleistung des Agenten zusätzlich.
Wie die oben aufgeführten Resultate zeigen, sind die Informationen, welche der Erfahrungspool bereitstellt, für den Prinzipal nützlich und sollten deshalb bei der Belohnung des Agenten berücksichtigt werden. Dadurch steigt der Nutzen des Prinzipals und die Arbeitsleistung des Agenten. Liegen die entsprechenden Informationen über die Arbeitsleistung nicht oder zu wenig präzise vor, weil kein Erfahrungspool vorhanden ist, so zeigen die obigen Überlegungen, welche Vorteile mit der Einführung eines entsprechenden Pools verbunden sind.
Allerdings stellt sich dabei die Frage, wie ein Vergleich des Nutzens des Prinzipals mit den Investitionskosten ausfällt. In diesem Zusammenhang hängt das Ergebnis insbesondere davon ab, welcher Zusammenhang zwischen den Kosten und der Varianz des Signals besteht. [Blickle, 1989; S. 102] stellt für den Fall, dass dem Agenten Kosten für die Bereitstellung der Informationen anfallen, fest: "In the case of costly signals general statements are not possible. The design of the optimal information system and payment schedule depends on the agent's risk-aversion, the variance of the random state of nature and the cost structure of the information system."
Zur Herleitung der genannten Ergebnisse werden einige der Funktionen aus den Prinzipal-Agent-Modellen M- und M+ mathematisch abgeleitet (1. Ordnung). Diese logische Analyse wird jedoch nicht für alle Parameter und Variablen durchgeführt, weil das Schwergewicht auf den Einfluss von zusätzlichen Informationen gelegt wird. Weitere interessante Erkenntnisse resultieren jedoch, wenn beispielsweise die Auswirkungen der Risikoaversion des Prinzipals und des Agenten in den Modellen M- und M+ untersucht werden.
Wie die Erweiterung des formalen Strommodells mit den Prinzipal-Agent-Modellen M- und M+ zeigt, müssen sehr viele Annahmen getroffen werden, um überhaupt eine Integration zu ermöglichen und den entsprechenden Grössen Werte zuweisen zu können. Bei einer Simulation muss beispielsweise von einer konkreten Nutzenfunktion und einem konkreten Wert der Risikoaversion ausgegangen werden. Hier gilt es allerdings zu beachten, dass vor allem die Tendenz eine wichtige Rolle spielt: So ist es beispielsweise unbedeutend, ob der Nutzen schlussendlich um "0.3" oder "0.31" Einheiten gesteigert wird oder ob der Agent eine Risikoaversion von "0.1" oder "0.11" hat. Wichtig ist beim Nutzen vor allem, ob er gesteigert wird und ob der Nutzen positiv ist. Analog kann der Wert der Risikoaversion lediglich darüber Auskunft gegen, ob es sich bei der betreffenden Partei um eine "tendenziell" risikoaverse oder risikoneutrale Person handelt. Bei der Herleitung der Ergebnisse werden diese Aspekte berücksichtigt, indem jeweils die relativen Veränderungen untersucht werden.
Sehr deutlich zeigt die Erweiterung des formalen Strommodells auf, dass bei der konkreten Ausformulierung von Prinzipal-Agent-Modellen sehr schnell verhältnismässig umfangreiche mathematische Zusammenhänge und Formeln resultieren. Der Umfang von Prinzipal-Agent-Modellen steigt zudem stark an, wenn zusätzliche Aspekte des darzustellenden Umweltausschnitts modelliert werden wollen. So kommt beispielsweise [Spremann, 1989; S. 17-30] zu ähnlichen Ergebnissen, wie sie sich auch aus dem Modell M+ ergeben, jedoch betrachtet er ausschliesslich einen risikoneutralen Prinzipal. Im Prinzipal-Agent-Modell M+ kann der Prinzipal sowohl zur Risikoneutralität als auch zu sehr hoher Risikoaversion tendieren; dieser Aspekt wird somit in M+ differenzierter modelliert, was sich jedoch durch umfangreichere mathematische Darstellungen erkauft werden muss.
[Holmström, 1979; S. 84] nennt in allgemeiner Form die Anforderungen an ein kostenloses "Kontrollinformationssystem" (Geschäftsergebnis und zusätzliche Informationen geben Aufschluss über die Aktion des Agenten), damit das betreffende System einen höheren Wert hat als ein System, welches keine zusätzlichen Informationen erhebt. Die vorgestellte Erweiterung des formalen Strommodells um das Prinzipal-Agent-Modell M+ zeigt diesen höheren Wert anhand eines konkreten Beispiels auf.