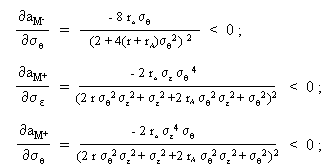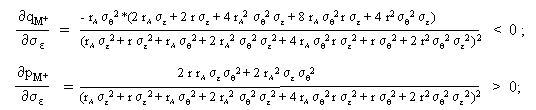Die drei Gleichungen zur Berechnung der Quoten bilden den Kern des formalen Strommodells. Die Quoten sind unter anderem von ihren Werten in der vorhergehenden Periode abhängig.
In diesem Kapitel werden Eigenschaften des funktionalen Zusammenhangs zwischen "Ft" und "Ft-1" mathematisch hergeleitet und beschrieben. Aufgrund der ähnlichen Struktur der drei Gleichungen gelten die aufgezeigten Merkmale analog bei den Quoten der Informatikabteilung und des Erfahrungspools.
Im formalen Strommodell gilt folgender funktionale Zusammenhang, und es wird von folgenden Voraussetzungen ausgegangen:

Der Parameter a und der Nichtlinearitätsfaktor werden bei den folgenden Untersuchungen als konstant vorausgesetzt. Bei der Wahl von "a " und "NLF" muss insbesondere berücksichtigt werden, dass Quoten mit Werten grösser oder gleich eins ausgeschlossen sind. Es darf bei gegebenem "a " und "NLF" kein Wert für "Ft-1" (im Intervall von null bis eins) existieren, so dass "Ft" aufgrund der obigen Funktion einen Wert grösser oder gleich eins annimmt. (Die nachfolgenden Untersuchungen gehen von stetigen Funktionen aus.)
Je mehr sich "Ft-1" dem Wert null nähert, desto kleiner wird auch "Ft":
![]()
[Kreutzberg, 1998] fordert, dass der Nichtlinearitätsfaktor "NLF" grösser als eins sein muss, um dadurch negative Quoten zu vermeiden. Dies ist ersichtlich, wenn auf der rechten Seite der (eingerahmten) Gleichung der Faktor "a Ft-1" vorgeklammert wird: Sämtliche Faktoren sind grösser als null, wenn der NLF grösser als eins ist. Würden hingegen Werte des NLFs kleiner als eins zugelassen werden, wäre der entsprechende Faktor und somit die Quote negativ.
Weiter ist erkennbar, dass durch das Vorklammern des Faktors "a Ft-1" der Parameter a als einziger Faktor Werte grösser als eins annimmt. Wird für a ein Wert kleiner als eins verwendet, so wird die Quote der vergangenen Periode immer mit einem Wert kleiner als eins multipliziert. Ein permanentes Absinken der Quote im Laufe der Zeit ist die Folge.
Notwendige Bedingung für ein Wachstum der Quote ist somit, dass a grösser als eins gewählt wird. Diese Bedingung ist zugleich hinreichend dafür, dass innerhalb eines gewissen Wertebereichs immer ein Wachstum stattfindet:
Voraussetzung: vgl. obige Bedingungen
Behauptung: Es existiert eine Quote F2, welche grösser ist als der Wert der Quote in der vorhergehenden Periode (F1).
Beweis: F2 > F1 Û (F2/F1) > 1
Þ Beweise, dass (F2/F1) grösser als eins ist.
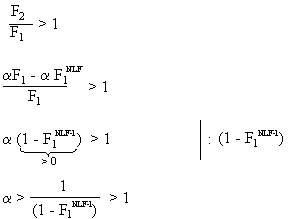
Bei vorgegebenem Parameter a wird sich immer ein Wert für F1 finden lassen (F1 sehr klein wählen), damit die (letzte) Ungleichung erfüllt ist. Somit gilt für sehr kleine Werte von F1 in jedem Fall, dass F2 grösser als F1 ist.
Je mehr sich "Ft-1" dem Wert eins annähert, desto kleiner wird "Ft":
![]()
Dieser extrem hohe "Dämpfungseffekt" stellt einen Kritikpunkt am formalen Strommodell dar, weil die betreffende Quote ceteris paribus nie über zwei Zeitperioden hinweg hohe Werte annehmen kann.
|
Die nebenstehende Abbildung stellt den funktionalen Zusammenhang zwischen "Ft" und "Ft-1" anhand eines Beispiels dar. Die Eigenschaften, wie sie oben mathematisch hergeleitet werden, sind dabei gut zu erkennen: Die Kurve schneidet die Abszisse bei den Werten null und eins, und weil a grösser als eins ist, nehmen tiefe Quoten in der nächsten Periode einen höheren Wert an. (Die Kurve wird also bei tiefen Werten von "Ft-1" oberhalb der gepunkteten Geraden verlaufen.) Bei einer stetigen Funktion bedeutet ein solcher Verlauf insbesondere, dass die Funktion einen Hochpunkt (Maximum) besitzt und dass ein Gleichgewichtspunkt existiert, bei welchem die |
|
Quote ceteris paribus ihren Wert nicht mehr ändern wird (Schnittpunkt der Geraden mit der Kurve).
Die mathematische Herleitung des Hochpunkts ergibt sich wie folgt:
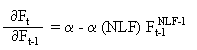
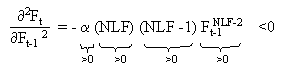
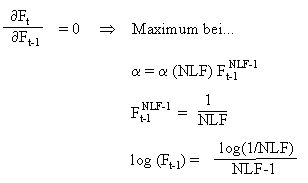
Der Gleichgewichtspunkt lässt sich wie folgt berechnen:
Die Quote ändert sich im Laufe der Zeit nicht; der Wert der vorhergehenden Periode wird gleich hoch sein wie in der aktuellen Periode. Daraus ergibt sich:
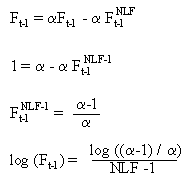
Die Ableitung 1. Ordnung der Funktion im Gleichgewichtspunkt beträgt:
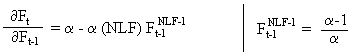
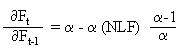
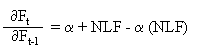
Bildet der Gleichgewichtspunkt zugleich den Hochpunkt (Maximum), dann muss folgende Bedingung gelten:
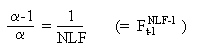
a + NLF - a (NLF) = 0
Falls der Hoch- und Gleichgewichtspunkt nicht zusammenfallen, können anhand des Parameters a und des Nichtlinearitätsfaktors trotzdem wichtige Aussagen abgeleitet werden: Der Hochpunkt wird vor dem Gleichgewichtspunkt erreicht, wenn gilt:
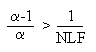
a + NLF - a (NLF) < 0
Das Maximum der Funktion befindet sich nach dem Gleichgewichtspunkt, falls gilt:
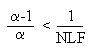
a + NLF - a (NLF) > 0
Diese Erkenntnisse lassen sich ableiten, wenn die Bedingungen für "Ft-1" beim Hochpunkt und beim Gleichgewichtspunkt einander gegenübergestellt werden oder die Ableitung 1. Ordnung im Gleichgewicht berücksichtigt wird (vgl. obige mathematische Umformungen).
Es gilt zu beachten, dass bei sämtlichen Schlussfolgerungen und mathematischen Umformungen in diesem Kapitel nicht auf die Kostenwachstumsrate "Kt" eingegangen wird. Die gefundenen Ergebnisse gelten sowohl bei einer Stagnation der Kosten als auch bei einer positiven oder negativen (konstanten) Kostenwachstumsrate.
In diesem Kapitel wird anhand einiger Beispiele bestätigt, was durch logisch/mathematische Schlussfolgerungen bereits hergeleitet wurde. Weiter werden ausgewählte Beispiele gezeigt, welche aufgrund von Computersimulationen zusätzliche Zusammenhänge und Eigenschaften vermuten lassen.
Bei der durchgeführten Computersimulation wurde wie folgt vorgegangen: Der Parameter a , der Nichtlinearitätsfaktor und der Startwert werden bei jedem Beispiel im voraus bestimmt und als Konstante vorgegeben. Die Werte werden derart gewählt, dass insbesondere die Steigung der Funktion im Gleichgewicht sehr verschieden ausfällt und dass jede Funktion die Voraussetzungen des formalen Strommodells (innerhalb der gültigen Wertebereiche) erfüllt. Anschliessend werden die Werte der Quote für die nächsten 300 Perioden via Tabellenkalkulation berechnet, und die Entwicklung wird in einem Diagramm (Abszisse: Zeit; Ordinate: Wert der Quote) dargestellt. Aufgrund dieser Grafik wird untersucht, ob im Laufe der Zeit gewisse Regelmässigkeiten erkannt werden können.
Ausgewählte Beispiele zur Entwicklung der Quote:
|
a |
NLF |
F0 |
F* |
Steigung bei F* |
Bemerkungen |
|
1.3 |
1.7 |
0.3 |
0.12320 |
+0.79 |
Die Quote konvergiert gegen das Gleichgewicht, wobei sämtliche Werte der Quote grösser als F* sind. |
|
2 |
1.8 |
0.1 |
0.42045 |
+0.2 |
Die Quote konvergiert gegen das Gleichgewicht, wobei sämtliche Werte der Quote kleiner als F* sind. |
|
2 |
1.8 |
0.47963 |
0.42045 |
+0.2 |
Die Quote konvergiert gegen das Gleichgewicht, wobei sämtliche Werte der Quote grösser als F* sind und der maximale Wert der Quote erreicht wird. |
|
1.1 |
5 |
0.99999 |
0.54910 |
+0.6 |
Die Quote konvergiert gegen das Gleichgewicht, wobei sämtliche Werte der Quote mit Ausnahme des Startwerts kleiner als F* sind. |
|
1.8 |
2.25 |
0.7 |
0.52270 |
0 |
Die Quote konvergiert gegen das Gleichgewicht, wobei sämtliche Werte der Quote mit Ausnahme des Startwerts kleiner als F* sind. |
|
3 |
1.5 |
0.00001 |
0.44444 |
0 |
Die Quote konvergiert gegen das Gleichgewicht, wobei sämtliche Werte der Quote kleiner als F* sind. |
|
10001 |
1.0001 |
0.7 |
0.36790 |
0 |
Die Quote konvergiert gegen das Gleichgewicht, wobei sämtliche Werte der Quote mit Ausnahme des Startwerts kleiner als F* sind. |
|
1.05 |
30 |
0.5 |
0.90034 |
-0.45 |
Die Computersimulation deutet darauf hin, dass sich der Wert ins Gleichgewicht einpendelt. Alternierend nimmt die Quote einen Wert grösser als F* bzw. kleiner als F* an, wobei sich der Abstand zu F* stets verkleinert. |
|
2 |
2.5 |
0.9 |
0.62996 |
-0.5 |
Die Computersimulation deutet darauf hin, dass sich der Wert ins Gleichgewicht einpendelt. |
|
2 |
2.5 |
0.6 |
0.62996 |
-0.5 |
analog wie beim vorherigen Beispiel. |
|
1.75 |
3.6 |
0.01 |
0.72189 |
-0.95 |
Die Computersimulation deutet darauf hin, dass sich der Wert ins Gleichgewicht einpendelt. |
|
1.8 |
3.5 |
0.8 |
0.72298 |
-1 |
Die Computersimulation deutet darauf hin, dass sich der Wert ins Gleichgewicht einpendelt. Allerdings scheint sich die Quote langsamer ans Gleichgewicht anzunähern wie in den vorhergehenden vier Beispielen. |
|
2 |
3 |
0.15 |
0.70711 |
-1 |
analog wie beim vorhergehenden Beispiel. |
|
1.25 |
9 |
0.85 |
0.62430 |
-1 |
analog wie beim vorhergehenden Beispiel. |
|
1.3 |
8 |
0.1 |
0.81101 |
-1.1 |
Die Computersimulation deutet darauf hin, dass sich die Quote einem 2-Perioden-Zyklus annähert, wobei die Quote wechselweise zwischen den Werten "0.76767" und "0.84117" pendelt. |
|
3 |
2.2 |
0.4 |
0.71328 |
-1.4 |
Die Computersimulation deutet darauf hin, dass sich die Quote einem 2-Perioden-Zyklus annähert, wobei die Quote wechselweise zwischen den Werten "0.47302" und "0.84115" pendelt. |
|
3 |
2.2 |
0.99 |
0.71328 |
-1.4 |
Die Computersimulation deutet darauf hin, dass die Entwicklung der Quote in den gleichen 2-Perioden-Zyklus mündet, wie beim vorhergehenden Beispiel. (unabhängig vom Startwert) |
|
2 |
3.5 |
0.5 |
0.75786 |
-1.5 |
Die Computersimulation deutet darauf hin, dass sich die Quote einem 4-Perioden-Zyklus annähert. Zudem lässt die Simulation vermuten, dass sich dieser Zyklus unabhängig vom Startwert einstellt. |
|
1.6 |
5.4 |
0.2 |
0.80018 |
-1.64 |
Aufgrund der Computersimulation kann nicht abgeleitet werden, ob und welchem Zyklus sich die Entwicklung der Quote annähert. |
|
1.3 |
11 |
0.999 |
0.86361 |
-2 |
Die Computersimulation lässt keine regelmässige Entwicklung erkennen. Auffällig ist bei diesem Szenario, dass sich die Quote in einem Zeitpunkt sehr stark an F* annähert (5 Perioden nahe bei F*), aber sich anschliessend wieder entfernt. |
|
1.1 |
50 |
0.95 |
0.95224 |
-3.9 |
Die Computersimulation lässt keine Aussagen über die Entwicklung der Quote zu. |
Es sei darauf verwiesen, dass mit der gewählte Untersuchungsmethode (Computersimulation) verschiedene Probleme verbunden sind:
In diesem Sinne dürfen die abgeleiteten Schlussfolgerungen aus der Computersimulation nur als ein erster Eindruck über mögliche Entwicklungen der Quoten verstanden werden. Ausnahme bilden selbstverständlich jene Eigenschaften und Zusammenhänge, welche in dieser Arbeit logisch/mathematisch begründet werden.
[Kreutzberg, 1998] leitet wichtige Funktionen des formalen Strommodells nach diversen Variablen ab und interpretiert die gefundenen Ergebnisse. Im folgenden werden die mathematischen Umformungen nochmals wiedergegeben. Um die Auswirkungen bei Veränderung der Quotendifferenz zu erkennen (analog zur Veränderung der Wachstumsrate), sind zwei weitere mathematische Ableitungen (mit "*" gekennzeichnet) beigefügt.

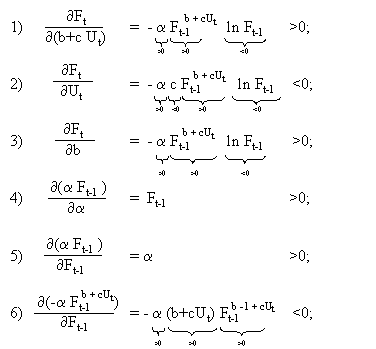
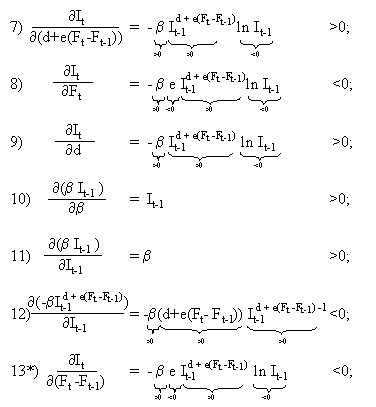
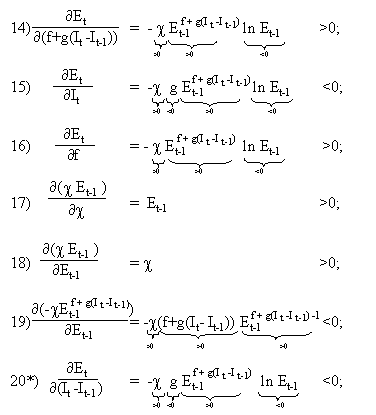
Das formale Strommodell wird erweitert mit den Prinzipal-Agent-Modellen M- und M+. Diese Modelle werden derart spezifiziert, dass sich die Arbeitsleistung und die Belohnungsfunktion des Agenten sowie der erwartete Nutzen des Prinzipals konkret berechnen lassen. Die Ergebnisse, wie sie im Kapitel " Integration von Prinzipal-Agent-Modellen ins formale Strommodell" beschrieben werden, beruhen auf den folgenden mathematischen Umformungen und Beweisen.
9.4.1 Erwartungswert bei CARA-Nutzenfunktionen
Eine Nutzenfunktion G der Form "G:= G(w) = 1 - e - r w " wird als CARA-Nutzenfunktion bezeichnet (Constant Absolute Risk Aversion). Der Parameter "r" steht für die Risikoaversion der entsprechenden Partei, und der Wert der Variablen "w" ist in Prinzipal-Agent-Modellen unter anderem von Zufallsvariablen abhängig. Da es sich bei Prinzipal-Agent-Modellen immer um stochastische Modelle handelt, wird typischerweise der Nutzen des Prinzipals und des Agenten ex ante nicht bekannt sein. Es kann jedoch der Erwartungswert der betreffenden Grössen ausgerechnet werden.
In den beiden vorgestellten Prinzipal-Agent-Modellen M- und M+ handelt es sich bei den stochastischen Grössen stets um normalverteilte Zufallsvariablen mit Erwartungswert 0 und Varianz s 2, welche schliesslich in CARA-Nutzenfunktionen einfliessen. Die Erwartungswerte der Nutzenfunktionen lassen sich auf der Grundlage der folgenden Beweise berechnen:
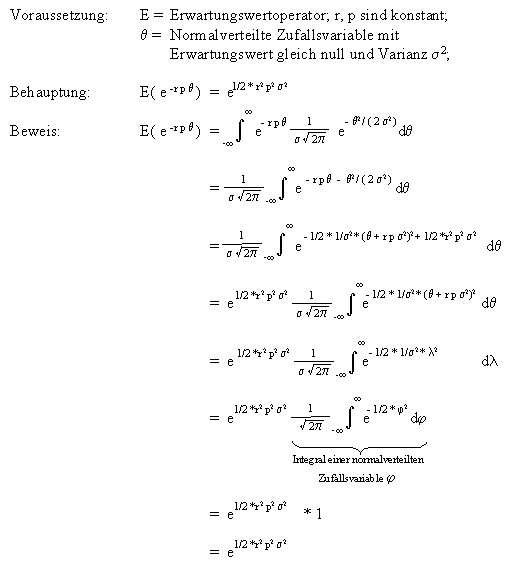
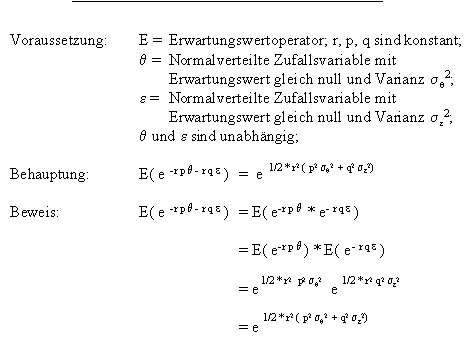
9.4.2 Prinzipal-Agent-Modell M-
Das Prinzipal-Agent-Modell M- bildet die Grundlage fürs Prinzipal-Agent-Modell M+. Die Ergebnisse fürs Prinzipal-Agent-Modell M- können auf analogem (einfacherem) Wege wie im Modell M+ hergeleitet und mathematisch begründet werden (® vgl. nächsten Abschnitt).
9.4.3 Prinzipal-Agent-Modell M+
Im Prinzipal-Agent-Modell M+ hat der Prinzipal formal folgendes Problem zu lösen:

Die Bedeutung der einzelnen Parametern und Variablen sowie die dazugehörenden Bedingungen werden im Kapitel "Erweiterung des Strommodells" in den entsprechenden Abschnitten aufgeführt.
Anhand der Anreiznebenbedingung lässt sich ein Zusammenhang zwischen der Arbeitsleistung (a) und den Parametern zur Berechnung der variablen Lohnanteile (p, q) herleiten:
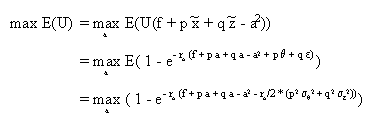
Die obige CARA-Nutzenfunktion wird maximiert, indem der Exponent (h) minimiert wird:
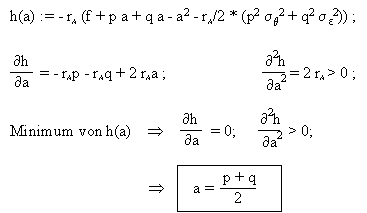
Es gilt zu beachten, dass bei der Anreiznebenbedingung die Grössen "p" und "q" als Parameter und nicht als Variablen behandelt werden. Der Agent hat bei der Wahl seines Arbeitsniveaus keinen Einfluss auf diese Grössen und wird sie als konstant und vorgegeben betrachten.
Eine Auswertung der Teilnahmebedingung ergibt:
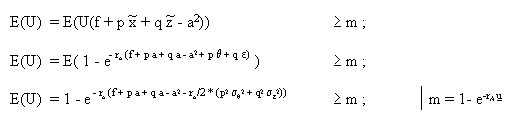
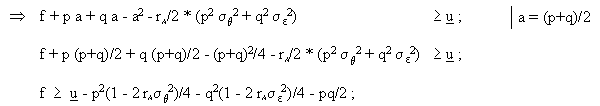
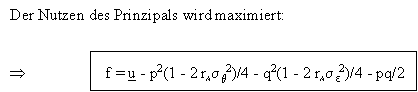
Schliesslich wird die Zielfunktion des Prinzipals ausgewertet, woraus folgende Ergebnisse resultieren:
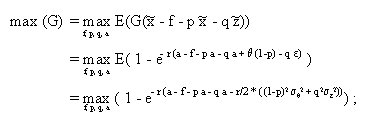

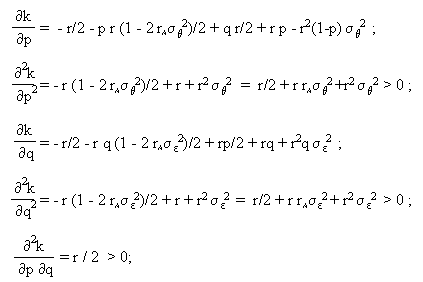
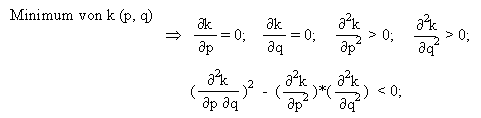
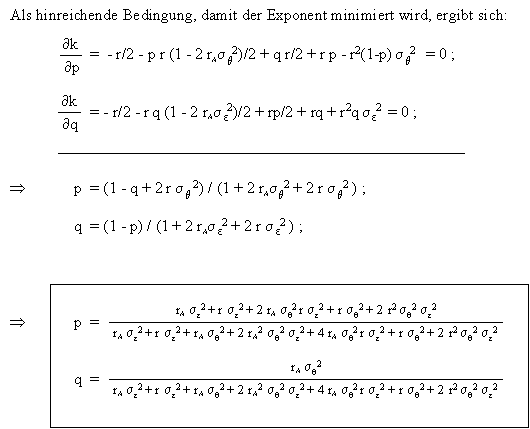
9.4.4 Arbeitsleistung in M- und M+
Die Arbeitsleistungen, welche der Agent in den Prinzipal-Agent-Modellen M- und M+ wählen wird, lassen sich aufgrund der Risikoaversionen (r und rA) sowie den Varianzen der Zufallsvariablen (s q , s e ) berechnen. Werden die Arbeitsleistungen aus M- und M+ miteinander verglichen, so zeigt sich, dass der Agent ein höheres Arbeitsniveau wählt, wenn seine Belohnung von zusätzlichen Informationen (® M+) abhängig gemacht wird:

9.4.5 Mathematische Ableitungen erster Ordnung in M- und M+
Einige Erkenntnisse, welche im Kapitel "Integration von Prinzipal-Agent-Modellen ins formale Strommodell" erwähnt werden, basieren auf mathematischen Ableitungen erster Ordnung von Funktionen aus den Prinzipal-Agent-Modellen M- und M+: